Question

A petrol tank is in the shape of a cylinder with hemisphere of same radius attached to both ends. If the total length of the tank is $6m$ and the radius is $1m$, what is the capacity of the tank in litres.

Answer 1

Hint: The petrol tank is in the shape of a cylinder with two hemispheres of same radii attached to the both sides. The capacity of the tank is equal to the total volume of the tank. Volume of the tank is equal to the sum of the volumes of the cylinder and two hemispheres.

Complete step-by-step answer:
Let us note down the given data.
A petrol tank is in the shape of a cylinder with hemisphere of same radius attached to both ends.
The total length of the tank is $6m$
 The radius is $1m$.
Here the radius refers to the radius of the hemisphere and the cylinder also.
So, let us draw the diagram as per the above data,

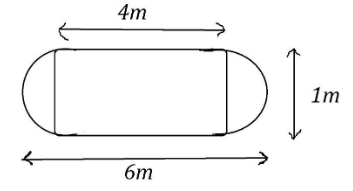
As the total length of the tank is $6m$ and the radius of the hemisphere is $1m$,
The length of the cylinder is $6 - 2\left( 1 \right) = 4m$
Now the volume of the tank is equal to the sum of the volumes of cylinder and two hemispheres.
Volume of the cylinder $ = \pi {r^2}h$
As we know the value of $r$ is $1$ and $h$ is $4$.
Substitute in the above formula,
Volume of cylinder $ = \pi \times {1^2} \times 4$
                $ = 4\pi $
Now, volume of hemisphere $ = \dfrac{2}{3}\pi {r^3}$
Substituting the values, we get,
Volume of hemisphere $ = \dfrac{2}{3}\pi {\left( 1 \right)^3}$
                       $ = \dfrac{{2\pi }}{3}$
Now, the capacity of the tank $ = $ Volume of the tank
                          $ = $ Volume of cylinder $ + $ $2 \times $ Volume of hemisphere
                          \[
   = 4\pi + 2 \times \dfrac{{2\pi }}{3} \\
   = \dfrac{{12\pi + 4\pi }}{3} \\
   = \dfrac{{16\pi }}{3} \\
 \]
We know the value of $\pi $ as $\dfrac{{22}}{7}$, if we substitute that in the above, we get,
Volume of the tank $ = \dfrac{{16}}{3} \times \dfrac{{22}}{7}$
                 $
   = \dfrac{{352}}{{21}} \\
   = 16.761{m^3} \\
 $
And we are asked to find out the capacity of the tank in litres. So, we know that $1{m^3} = 1000litres$. Apply in the above answer, we get
Volume of the tank or Capacity of the tank $ = 16.761 \times 1000$
      $ = 16761litres$.
Hence the capacity of tank in litres is $16761litres$

Note: This type of mensuration problem can be solved easily when we get a clear idea about the shapes of the solids that are involved in the body. We are able to solve this problem in other ways also. Anyways we are calculating the volume of hemisphere and multiplying it with two to get the volume of two hemispheres. But we can directly find the volume of the sphere as those two hemispheres are identical. It will also give the same answer.