Question

A piece of rod (7/8) meter long is broken into two pieces. One piece was (1/4) meter long. How long is the other piece?

Answer 1

Hint – In this particular type of question use the property that the original length of the rod is the sum of the length of the two pieces in which it is broken so use this concept to reach the solution of the question.

Complete step-by-step answer:

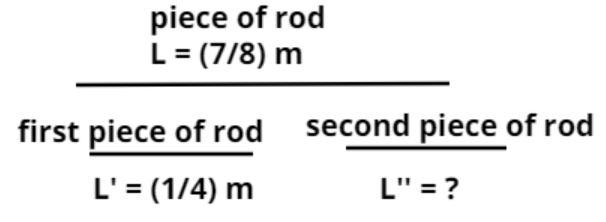
Given data:
Actual length of a piece of rod = (7/8) meter.
Let it be denoted by L.
Therefore, L = (7/8) meter.
Now this piece of rod is broken into two pieces.
The length of the first piece of rod is = (1/4) meter.
Let it be denoted by L’.
Therefore, L’ = (1/4) meter.
So we have to find out the length of the other piece of rod.
Now let the length of the other piece of rod be L’’.
So the original length of the rod is the sum of the length of the two pieces in which it is broken.
So the original length of the rod = length of the first piece of the rod + length of the second piece of the rod.
Now substitute the variables we have,
Therefore, L = L’ + L’’
Now substitute the values in the above equation we have,
Therefore, $\dfrac{7}{8} = \dfrac{1}{4} + L''$
Now take (1/4) to the L.H.S of the above equation we have,
$ \Rightarrow \dfrac{7}{8} - \dfrac{1}{4} = L''$
Now take 8 as LCM we have,
$ \Rightarrow \dfrac{{7 - 2}}{8} = L''$
Now simplify the above equation we have,
$ \Rightarrow L'' = \dfrac{5}{8}$ Meters.
So the length of the other piece of the rod is (5/8) meter.
So this is the required answer.

Note – Whenever we face such types of questions always draw the pictorial representation of the given problem statement as above it will give us a clear picture of what we have to calculated so, apply the formula as above applied and substitute the values and simplify as above we will get the required length of the other piece of rod.