Question

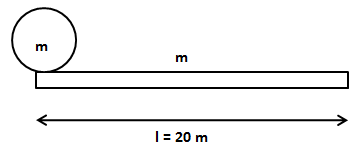
A plank of length 20m and mass 1 kg is kept on a horizontal smooth surface. A cylinder of mass of 1 kg is kept near one end of the plank. The coefficient of friction between the two surfaces is 0.5. Plank is suddenly given a velocity 20 m/s towards the left. Find the time which plank and cylinder separate.

Answer 1

Hint: Calculate the frictional force exerted on the cylinder and then determine the acceleration due to frictional force. Use the kinematic equation to determine the time taken to separate the cylinder from the plank. Take the value of acceleration as negative since it is the deceleration.

Formula used:
\[{f_k} = {\mu _k}mg\]
Here, \[{\mu _k}\] is the coefficient of kinetic friction, m is the mass of the body and g is the acceleration due to gravity.
\[s = ut + \dfrac{1}{2}a{t^2}\]
Here, s is the distance, u is the initial velocity, a is the acceleration and t is the time.

Complete step by step answer:
When we give the plank a sudden velocity, the cylinder on the plank will move towards the right. The only force that acts on the cylinder will be the kinetic friction between cylinder and plank.
Let’s express the kinetic friction between the cylinder and plank as follows,
\[{f_k} = {\mu _k}mg\]
Here, \[{\mu _k}\] is the coefficient of kinetic friction, m is the mass of the cylinder and g is the acceleration due to gravity.
Substituting 0.5 for \[{\mu _k}\], 1 kg for m and \[10\,{\text{m/}}{{\text{s}}^2}\] for g in the above equation, we get,
\[{f_k} = \left( {0.5} \right)\left( 1 \right)\left( {10} \right)\]
\[ \Rightarrow {f_k} = 5\,{\text{N}}\]
We can determine the deceleration of the cylinder using Newton’s second law as,
\[a = \dfrac{{{f_k}}}{m}\]
Substituting 5 N for \[{f_k}\] and 1 kg for m in the above equation, we get,
\[a = \dfrac{5}{1}\]
\[ \Rightarrow a = 5\,{\text{m/}}{{\text{s}}^2}\]
Now, let’s express the distance moved by the cylinder using kinematic equation as follows,
\[s = ut + \dfrac{1}{2}a{t^2}\]
Here, u is the initial velocity and t is the time.
Substituting 20 m for s, 20 m/s for u and \[ - 5\,{\text{m/}}{{\text{s}}^2}\] for a in the above equation, we get,
\[20 = 20t + \dfrac{1}{2}\left( { - 5} \right){t^2}\]
\[ \Rightarrow 2.5{t^2} - 20t + 20 = 0\]
\[ \Rightarrow {t^2} - 8t + 8 = 0\]
Solving the above equation using the formula, \[x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\], we have,
\[t = \dfrac{{ - \left( { - 8} \right) \pm \sqrt {{{\left( { - 8} \right)}^2} - 4\left( 1 \right)\left( 8 \right)} }}{{2\left( 1 \right)}}\]
\[ \Rightarrow t = 6.83\,{\text{s}}\]
Therefore, the plank and cylinder will separate after 6.83 seconds.

Note:
The acceleration due to frictional force is known as deceleration and it has negative sign since it decreases the velocity of the body.
The above equation will give two values of time but the other value has negative sign.
But since time cannot have the negative sign, we have omitted the second value of time.