Question

A plano-convex lens fits exactly into a Plano-concave lens. Their plane surfaces are parallel to each other. If lenses are made of different materials of refractive indices ${\mu _1}$ and ${\mu _2}$ and $R$ is the radius of curvature of the curved surface of the lenses, then the focal length of the combination is
A. $\dfrac{R}{{2({\mu _1} + {\mu _2})}}$
B. $\dfrac{R}{{2({\mu _1} - {\mu _2})}}$
C. $\dfrac{R}{{({\mu _1} - {\mu _2})}}$
D. $\dfrac{R}{{({\mu _2} - {\mu _1})}}$

Answer 1

Hint: For the different optical measurement the lenses of different focal lengths are used. The manufacturers of the lenses use the lens maker’s formula to calculate the desired focal length of the lens which is to be manufactured for the particular application. Lens maker’s formula can be used for all types of the lens like the concave lens, convex lens and Plano-concave, and plano-convex lenses.

Complete step-by-step solution:

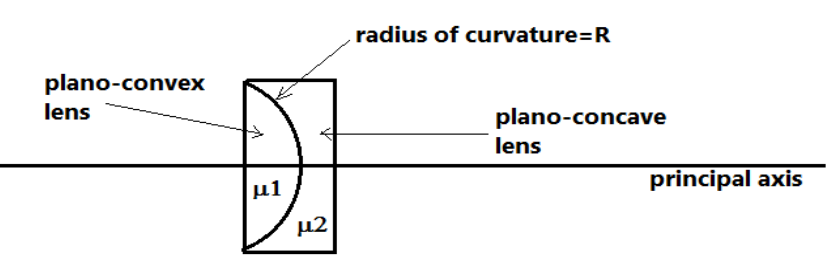
We all know the lens maker’s formula for the lenses.
That is,
$\dfrac{1}{f} = \left( {\mu - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
Where $f = $ focal length (half the radius of curvature)
$\mu = $ refractive index of the material used
${R_1} = $ radius of curvature of sphere 1
${R_2} = $ radius of curvature of sphere 2
Now we know that for the Plano-concave and plano-convex lenses, there is only one radius of curvature so the formula for the two given lenses will be modified as follows,
The lens maker’s formula for the plano-convex lens,
$\dfrac{1}{{{f_1}}} = \left( {{\mu _1} - 1} \right)\left( {\dfrac{1}{R}} \right)$, where $R = $radius of curvature
And ${f_1} = $focal length of the plano-convex lens,
${\mu _1} = $refractive index for the material of the plano-convex lens.
Now, the lens maker’s formula for the Plano-concave lens
$\dfrac{1}{{{f_2}}} = - \left( {{\mu _2} - 1} \right)\left( {\dfrac{1}{R}} \right)$ , where $R = $radius of curvature
And ${f_2} = $focal length of the Plano-concave lens,
${\mu _2} = $refractive index for the material of the Plano-concave lens.
And we have seen in the question that there is a combination of both the lenses so for the combination we have to find the equivalent focal length of the combination of the two lenses.
So, the equivalent focal length of the combination,
$\dfrac{1}{{{f_{eq}}}} = \left( {\dfrac{1}{{{f_1}}} + \dfrac{1}{{{f_2}}}} \right)$
$ \Rightarrow \dfrac{1}{{{f_{eq}}}} = \left( {{\mu _1} - {\mu _2}} \right)\left( {\dfrac{1}{R}} \right)$
${f_{eq}} = \dfrac{R}{{({\mu _1} - {\mu _2})}}$
So, option (C) is the correct answer.

Note: Plano-convex lenses are the lenses having one surface as a convex lens and another is plane. They have a positive focal length and can be designed for the infinite conjugate (parallel light) use or also can be used for simple-imaging in the non-critical applications.
Plano-concave lenses are the lenses having one surface as a concave lens and another surface is plane. Their focal length is negative and they can be used in light projection, beam expansion, or to increase the focal length of an optical system.