Question

A plano-convex lens is made of a material of refractive index \[n\]. When a small object is placed $30cm$ away in front of the curved surface of the lens, an image of double the size of the object is produced. Due to reflection from the convex surface of the lens, another faint image is observed at a distance of $10cm$ away from the lens. Which of the following statement (s) is (are) true?
A) The refractive index of the lens is $2.5$.
B) The radius of the curvature of the convex surface is $45cm$.
C) The faint image is erect and real.
D) The focal length of the lens is $20cm$.

Answer 1

Hint: In this question, a plano-convex lens is given. There are two images observed in this question. So, there are two different cases for two different images. The distance of the first image (double in size) from the lens will be found by using the formula of magnification $\dfrac{v}{u} = m$. We can find focal lengths in both cases by using Lens formula $\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$. The focal length from the first case gives the focal length of the lens and the focal length from the second case can give us the radius of curvature. We can use Lens Maker’s formula for a plano-convex lens $\dfrac{1}{{{f_1}}} = \dfrac{{(n - 1)}}{R}$ to find the refractive index of the lens.

Complete step by step answer:
The above figure shows the ray diagram of a plano-convex lens. In this diagram \[O\] shows the object at\[30cm\]. In this diagram \[I\] shows the image due to refraction which is double in size. In the diagram, there is one more image\[{I^{'}}\]. \[{I^{'}}\] shows the faint image due to reflection and placed at \[10cm\] from the lens.

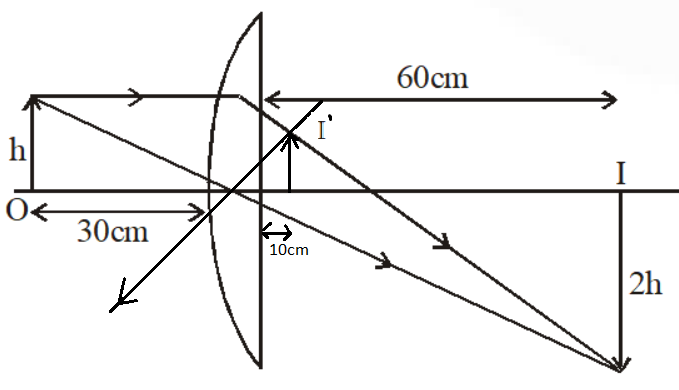
We have a plano-convex lens. A small object is placed at the distance $u = 30cm$ from the curved surface of the lens. The image of this object is doubled i.e. the image is magnified twice. So, we can find the distance of the image $v$ from the curved surface of the lens by using the formula of magnification-
$\dfrac{v}{u} = m$
Where $v$ is the distance of the image from the curved surface and $m$ is the magnification.
So, putting $u = - 30cm$ and $m = - 2$ in the formula of magnification.
$
  \dfrac{v}{{ - 30}} = - 2 \\
   \Rightarrow v = ( - 30) \times ( - 2) \\
   \Rightarrow v = 60cm \\
$
There are two cases in this question. In the first case, we get the image that is double in the size at $60cm$ from the curved surface. In the second case, the faint image due to the reflection is observed at $10cm$ from the curved surface. So, in both cases $u = 30cm$is the same but the $v$is different. So, the focal lengths are also different in both cases.
Now, let us take the case I.
Case I- When the size of the image is doubled and $v = 60cm$. Let the focal length of the lens is ${f_1}$ in this case. So, using the Lens formula, we get-
$\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$
Putting $v = 60,u = 30, f = {f_1}$ in the Lens formula, we get-
$ \dfrac{1}{{60}} + \dfrac{1}{{30}} = \dfrac{1}{{{f_1}}} $
On simplification,
$\Rightarrow \dfrac{{1 + 2}}{{60}} = \dfrac{1}{{{f_1}}} $
$ \Rightarrow \dfrac{3}{{60}} = \dfrac{1}{{{f_1}}} $
On further simplification,
$ \Rightarrow \dfrac{1}{{20}} = \dfrac{1}{{{f_1}}} $
$ \Rightarrow {f_1} = 20cm $
So, in case I, the focal length of the lens is $20cm$.
Now, let us take the case II.
In case II- When the faint image is observed due to reflection and $v = 10cm$. Let the focal length of the lens is ${f_2}$ in this case. So, using the Lens formula, we get-
$\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$
Putting $v = 10,u = - 30,f = {f_2}$ in the Lens formula, we get-
$ \Rightarrow \dfrac{1}{{10}} - \dfrac{1}{{30}} = \dfrac{1}{{{f_2}}} $
On simplification,
$ \Rightarrow \dfrac{{3 - 1}}{{30}} = \dfrac{1}{{{f_2}}} $
$ \Rightarrow \dfrac{2}{{30}} = \dfrac{1}{{{f_2}}} $
on further simplifications,
$ \Rightarrow \dfrac{1}{{15}} = \dfrac{1}{{{f_2}}}$
$ \Rightarrow {f_2} = 15cm $
So, in case II, the focal length of the lens is $15cm$.
Now, if \[f\] is the focal length of the lens and \[R\] is the radius of curvature then we know that
${f_2} = \dfrac{R}{2}$
Or we can write,
$R = 2 \times {f_2} $
On substituting the value $f_2$
$ \Rightarrow R = 2 \times 15$
On simplification,
$ \Rightarrow R = 30cm$
Now, using Lens Maker Formula for a plano-convex lens for case I, we get-
$\dfrac{1}{{{f_1}}} = \dfrac{{(n - 1)}}{R}$
Or we can write
$ {f_1} = \dfrac{R}{{n - 1}} $
On substituting the corresponding values,
$ \Rightarrow 20 = \dfrac{{30}}{{n - 1}} $
On simplification,
$ \Rightarrow n - 1 = \dfrac{{30}}{{20}} $
$ \Rightarrow n - 1 = 1.5 $
On further simplification,
$ \Rightarrow n = 1.5 + 1 $
$ \Rightarrow n = 2.5 $

Therefore, the radius of curvature of the plano-convex lens is \[30cm\]. The focal length of the plano-convex lens \[{f_1}\] is \[20cm\]. Hence, options A and D are correct.

Note:
The focal length from the first case is equal to the focal length of the plano-convex lens because the image in the first case is observed due to refraction. The image from the second case gives us the radius of curvature because the second image is observed due to reflection. In Lens Maker’s formula $\dfrac{1}{f} = (n - 1)\left[ {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right]$, there are two radii of curvature. This is because both the surfaces of the lens are curved surfaces. In the plano-convex lens. One of the surfaces is curved and the other surface is the plane mirror. So, Lens Maker’s formula can be modified to $\dfrac{1}{{{f_1}}} = \dfrac{{(n - 1)}}{R}$.