Question

A point $P$ is the contact point of a wheel on the ground that rolls on the ground without slipping. The value of displacement of the point $P$, when wheel completes half of rotation(if radius of wheel is 1m) is
A. $2m$
B. $\sqrt {{\pi ^2} + 4m} $
C. $\pi m$
D. $\sqrt {{\pi ^2} + 2m} $

Answer 1

Hint: Displacement provides the straight-line distance from starting position to end position.
If the wheel completes half rotation, the value of the displacement of the point p will be equal to half of the total displacement of the point
First, we have to draw the positional vector by using the given question then we can find the value of the displacement.

Complete answer:
Displacement is that it coincides with elementary movement along any arbitrary trajectory. At the same time, we do not know for sure whether this change is a straight line, or the shortest distance, or a stationary value in the sense of a geodesic line - we simply postulate, following Newton, that these two forms coincide as the movement tends to zero.
It turns out that the most important thing for displacement is to be not so much the shortest as to not depend on the measuring paths. In this case, a physical process is suitable for displacement as a form - the movement of a light beam in a vacuum.
The mathematical definition of displacement is
\[\Delta x = {x_i} - {x_f}\]
\[{x_f}\] is a vector final position.
\[{x_i}\] is a vector initial position.
From the origin of the coordinate system we can draw the positional vector

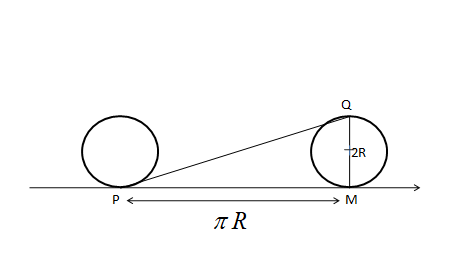
From the above diagram we can find the displacement PQ, is as follows,
\[PQ = \sqrt {{{\left( {PM} \right)}^2} + {{\left( {QM} \right)}^2}} \]
Now substitute the \[PM\]and \[QM\]in the above equation we get as follows,
\[PQ = \sqrt {{{\left( {\pi R} \right)}^2} + {{\left( {2R} \right)}^2}} \]
Substituting $R=m$,
Now solving the above equation will give,
\[PQ = \sqrt {{\pi ^2} + 4} \]

Therefore, the correct answer is option (B).

Note:
> The displacement is defined as the shortest distance among the two points.
> Since, the point P is the point that is directly in contact to the ground , we know that if the wheel is not slipping, that is, it is doing pure rolling then the Velocity of that particle will be zero
> The displacement may be positive or negative and it is a vector quantity.