Question

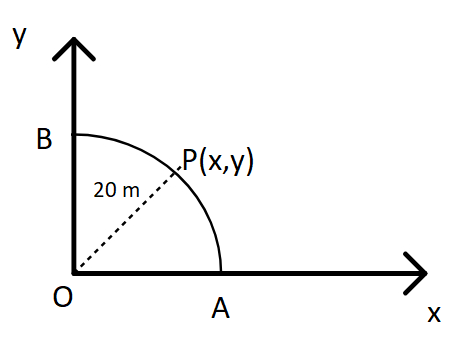
A point P moves in counter clockwise direction on a circular path as shown in the figure. The movement of 'P' is such that it sweeps out a length $s = t^3 + 5$, where s is in meters and t is in seconds. The radius of the path is 20 m. The acceleration of 'P' when t = 2s is nearly:

Answer 1

Hint: We are given the distance covered as a function of time. This will give the tangential acceleration of the body. For anybody to perform circular motion, there exists a centripetal acceleration that points to the centre of the circle.
Formula used:
The acceleration of any body performing circular motion towards the centre of the circle is given as:
$a_c = \omega^2 r = \dfrac{v^2}{r}$
where v is the velocity of circular motion.

Complete answer:
Our point is performing two types of acceleration here. One is tangential, one is radial. We first calculate the tangential acceleration by using the formula for s. We differentiate it once, we get the velocity:
$v = \dfrac{ds}{dt} = 3t^2 = 3.(2)^2 = 12 $ m/s.
The tangential acceleration is obtained by differentiating this:
$\dfrac{d^2 s}{dt^2} = 6 (2) = 12 m/s^2$
The radial acceleration is obtained as:
$a_c = \dfrac{(12)^2}{(20)} = 7.2 ms^{-2}$
where substitution for velocity at t= 2s has been made.
Now the resultant of these two accelerations will give us the required acceleration:
$a = \sqrt{ {a_t}^2 + {a_c}^2 } = \sqrt{ {12}^2 + {7.2}^2 } = 13.99 ms^{-2}$
This is the value of acceleration after t=2s of P.
Additional Information:
When a body undergoes uniform circular motion, the body possess constant linear velocity (in magnitude) the direction of the velocity changes at all points. Therefore, the body possesses certain acceleration pointing towards the centre. As the body has been given to cover some distance according to the given equation with respect to time, it undergoes some acceleration in the linear velocity too.

Note:
Looking at the equation of distance s one might rush to calculate the acceleration and declare the obtained value as the result but that is just the tangential acceleration. Acceleration is a vector quantity, the resultant of the two vectors, tangential and centripetal will give the total acceleration.