Question

A pole of height $4m$ is kept in front of a vertical plane mirror of length $2m$. The lower end of the mirror is at a height of $6m$from the ground. The horizontal distance between the mirror and the pole is $2m$. Up to what minimum and maximum heights a man can see the image of the top of the pole at a distance of $4m$ standing on the same horizontal line which is passing through the pole and the horizontal point below the mirror?

Answer 1

Hint: A plane mirror reflects light in such a way that the angle of incidence is equal to the angle of reflection. Since the horizontal distance of the man, mirror and pole is fixed, the maximum and the minimum angle of incidence also have a definite value, which could be found by joining the top of the pole to the ends of the mirror.

Complete step by step answer:
 Given that-
Height of pole$ = 4m$
Length of the mirror$ = 2m$
Height of the lower end of the mirror= 6m
Horizontal distance between the mirror and pole$ = 2m$
Horizontal distance of man from the mirror$ = 4m$


For minimum distance-
Let the minimum angle of incidence and reflection be$\phi $.
In triangles, PQS and QOT the angle$\phi $ is made, thus they are similar.
For triangle PQS,
$\tan \phi = \dfrac{{QT}}{{OT}}$
QT is the distance between the top of the pole and the lower end of the mirror. It is equal to $2m$.
OT is the horizontal distance between pole and the mirror it is equal to $2m$.
Therefore,
$\tan \phi = \dfrac{2}{2} = 1$
Angle of incidence,$\phi = 45^\circ $
We know that $\tan \phi = 1$
In triangle, PQS ,

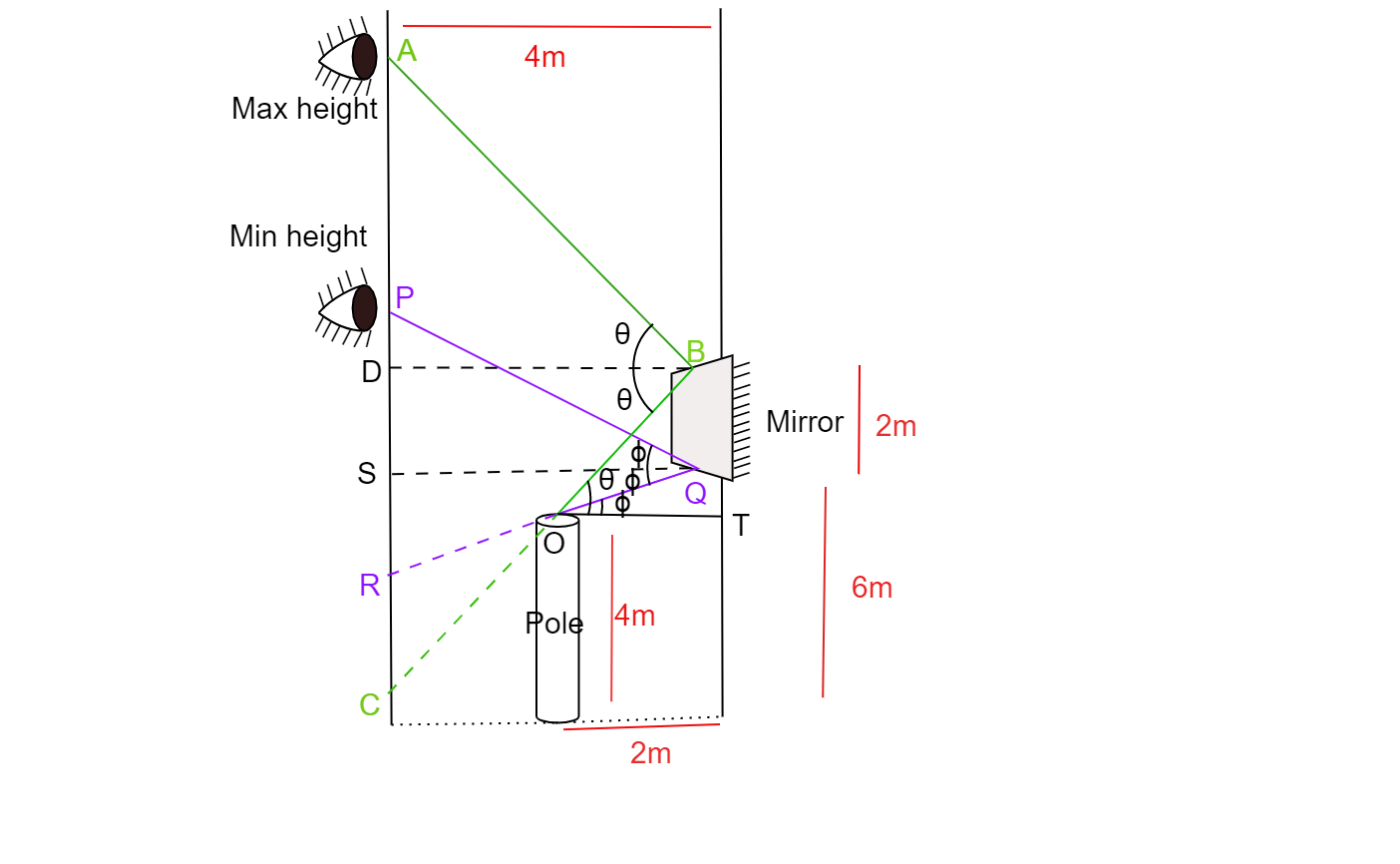
$\tan \phi = \dfrac{{PS}}{{SQ}}$
Given, $SQ = 4$
Therefore, $PS = SQ\tan \phi $
$PS = 4 \times 1$
$PS = 4m$
The minimum vertical distance$6 + 4 = 10m$
For maximum distance-
Let the maximum angle of incidence and reflection be $\theta $
In triangle BOT,
The angle O is equal to $\theta $.
Thus, $\tan \theta = \dfrac{{BT}}{{OT}} = \dfrac{{BQ + QT}}{{OT}}$
$\tan \theta = \dfrac{{2 + 2}}{2} = \dfrac{4}{2} = 2$
$\tan \theta = 2$
Given, $DB = 4m$
In triangle ABD,
$\tan \theta = \dfrac{{AD}}{{DB}}$
Therefore, $AD = DB\tan \theta $
$AD = 4 \times 2 = 8m$
The maximum vertical distance $ = 6 + 2 + 8 = 16m$
The minimum distance where man can view the top of the pole is $10m$ and the maximum distance is $16m$.

Note:
A plane mirror produces a virtual, upright and same sized image of an object. The image appears to be situated at equal distance from the mirror surface. As the object distance is increased, plane mirrors can produce equally distant images, even vertically. The angle of incidence can vary from $0^\circ $to$90^\circ $.