Question

A polygon has 6 sides. How would I find the measure of each exterior and interior angle?

Answer 1

Hint: We recall definitions of interior angle and exterior angle of a polygon. We can only find all measures of all interior and exterior angles if the polygon is regular. We recall that interior angle of a regular polygon is $\dfrac{{{180}^{\circ }}\left( n-2 \right)}{n}$ and measure of exterior angle as ${{180}^{\circ }}-\dfrac{{{180}^{\circ }}\left( n-2 \right)}{n}$. We use these formulas for $n=6$.\[\]

Complete step by step answer:
We know from geometry that a polygon closed and simple curve which is made up of joining distinct points by line segments. Those points are called vertices and those line segments are called sides. If the length of all sides is equal, then we call the polygon regular polygon. \[\]
We also know that the angle subtended by two sides of a polygon in the interior of the polygon and angle subtended in the exterior of the polygon by side and its adjacent extended side extended is called exterior angle. We show an interior and exterior angle of a regular polygon with 6 sides .\[\]

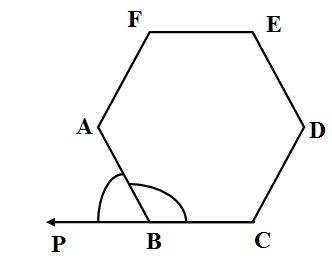
We see above the interior angle $\angle ABC$ and from sides $AB,AC$ and exterior angle $\angle ABP$ made by side with side $CB$ extended to $\overrightarrow{CP}$. \[\]
We know from angle sum property that the sum of interior angles of as ${{180}^{\circ }}\left( n-2 \right)$ and measure of all angles in a regular polygon is equal. So the measure of one interior angle is $\dfrac{{{180}^{\circ }}\left( n-2 \right)}{n}$. Since exterior and interior angles are supplementary to each other (like here $\angle ABC+\angle ABP={{180}^{\circ }}$ ) we have measure of one exterior angle as ${{180}^{\circ }}-\dfrac{{{180}^{\circ }}\left( n-2 \right)}{n}$. \[\]
We are given there are 6 sides. If the polygon is regular then measure of one interior angle is
\[\dfrac{{{180}^{\circ }}\left( n-2 \right)}{n}=\dfrac{{{180}^{\circ }}\left( 6-2 \right)}{6}=\dfrac{{{180}^{\circ }}\times 4}{6}={{30}^{\circ }}\times 4={{120}^{\circ }}\]
Then the measure of one exterior angle is
\[{{180}^{\circ }}-\dfrac{{{180}^{\circ }}\left( n-2 \right)}{n}={{180}^{\circ }}-{{120}^{\circ }}={{60}^{\circ }}\]

Note:
We note that if there are $n$ sides of a polygon then there are $n$ interior and $2n$ exterior angles. If we move from one vertex to another we shall meet $n$ exterior angles in one revolution. By exterior angle sum theorem their sum is ${{360}^{\circ }}$. So we can find alternatively the measure of one exterior angle as $\dfrac{{{360}^{\circ }}}{n}=\dfrac{{{360}^{\circ }}}{6}={{60}^{\circ }}$.