
Answer
441.3k+ views
Hint: The ratio of the potential difference across both the shunt resistances is equal to the ratio of the respective balancing lengths, i.e. $\dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{{{l}_{1}}}{{{l}_{2}}}$. The potential difference across a shunt resistance R is $V=\dfrac{ER}{(r+R)}$. Use these formulas to find the internal resistance of the cell.
Formula used:
$V=iR$
Complete step-by-step solution
Let us first understand the working of a potentiometer. To understand better, follow the given figure. This given figure is a simple setup of a potentiometer when it is used to measure the internal resistance of the unknown cell.
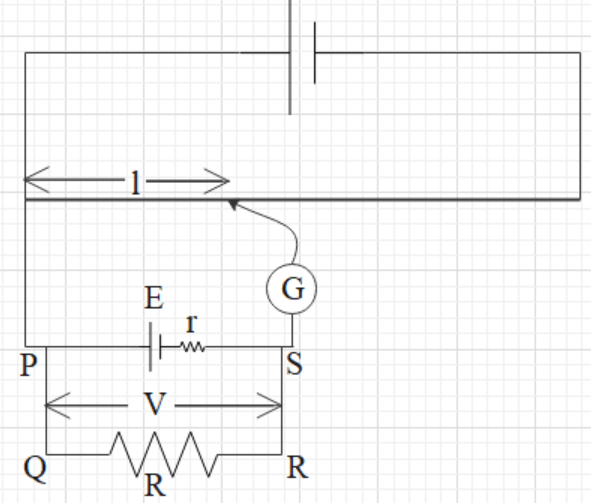
A potentiometer consists of a long wire of some known resistance and its total length is L (AB). It is connected to a cell and a potential difference is created across the wire.
J is a moveable point to find the balancing length. When there is zero current found in the galvanometer, the circuit is balanced.
When the circuit is balanced, the voltage (V) across the shunted resistance (R) is directly proportional to the balancing length (l) i.e. $V\propto l$.
Therefore, V=kl, where k is a constant.
When the circuit is balanced, $V=E-ir$ and V=iR, where i is the current in the circuit PQRS and r is the internal resistance of the cell (E).
This implies that E - ir = iR.
$\Rightarrow E=i(r+R)\Rightarrow i=\dfrac{E}{(r+R)}$.
Therefore,
$\Rightarrow V=E-ir=E-\left( \dfrac{E}{(r+R)} \right)r$
$\Rightarrow V=E\left( 1-\dfrac{r}{(r+R)} \right)$
$\Rightarrow V=\dfrac{ER}{(r+R)}$
Now, divide the numerator and the denominator by R.
$\Rightarrow V=\dfrac{\dfrac{ER}{R}}{\dfrac{(r+R)}{R}}=\dfrac{E}{\dfrac{r}{R}+1}$
When a resistance of infinity, let the voltage across the resistance be ${{V}_{1}}$ and the balancing length be ${{l}_{1}}$.
Therefore, ${{V}_{1}}=k{{l}_{1}}$ …. (i).
And ${{V}_{1}}=\dfrac{E}{\dfrac{r}{R}+1}$.
But, if $R\to \infty $ then $\dfrac{r}{R}\to 0$.
$\Rightarrow {{V}_{1}}=\dfrac{E}{0+1}=E$ …. (ii).
Let the voltage across the shunted resistance of 9.5$\Omega $ be ${{V}_{2}}$ and the balancing length be ${{l}_{2}}$.
Therefore, ${{V}_{2}}=k{{l}_{2}}$ …. (iii).
And ${{V}_{2}}=\dfrac{9.5E}{(r+9.5)}$ ….. (iv).
Divide equations (i) and (iii).
$\Rightarrow \dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{{{l}_{1}}}{{{l}_{2}}}$.
Here, ${{l}_{1}}$= 3cm and ${{l}_{2}}$= 2.85cm.
This gives us that
$\dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{3}{2.85}$.
Now, divide equations (ii) and (iv).
$\dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{E}{\dfrac{9.5E}{(r+9.5)}}=\dfrac{(r+9.5)}{9.5}$
But $\dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{3}{2.85}$.
Therefore,
$\dfrac{(r+9.5)}{9.5}=\dfrac{3}{2.85}$
$\Rightarrow 2.85(r+9.5)=3(9.5)$
$\Rightarrow 2.85r+27.075=28.5$
$\Rightarrow r=\dfrac{28.5-27.075}{2.85}=\dfrac{1.425}{2.85}=0.5\Omega $
Therefore, the internal resistance of the given cell is $0.5\Omega $
Hence, the correct option is C.
Note: Note that the emf of the unknown cell must always be less than the emf of the main cell. If the emf of the cell that is to be measured is more than the emf of the main cell, then the balancing length will be more than the length of the resistance wire and we will not be able to measure the emf of the cell.
Formula used:
$V=iR$
Complete step-by-step solution
Let us first understand the working of a potentiometer. To understand better, follow the given figure. This given figure is a simple setup of a potentiometer when it is used to measure the internal resistance of the unknown cell.

A potentiometer consists of a long wire of some known resistance and its total length is L (AB). It is connected to a cell and a potential difference is created across the wire.
J is a moveable point to find the balancing length. When there is zero current found in the galvanometer, the circuit is balanced.
When the circuit is balanced, the voltage (V) across the shunted resistance (R) is directly proportional to the balancing length (l) i.e. $V\propto l$.
Therefore, V=kl, where k is a constant.
When the circuit is balanced, $V=E-ir$ and V=iR, where i is the current in the circuit PQRS and r is the internal resistance of the cell (E).
This implies that E - ir = iR.
$\Rightarrow E=i(r+R)\Rightarrow i=\dfrac{E}{(r+R)}$.
Therefore,
$\Rightarrow V=E-ir=E-\left( \dfrac{E}{(r+R)} \right)r$
$\Rightarrow V=E\left( 1-\dfrac{r}{(r+R)} \right)$
$\Rightarrow V=\dfrac{ER}{(r+R)}$
Now, divide the numerator and the denominator by R.
$\Rightarrow V=\dfrac{\dfrac{ER}{R}}{\dfrac{(r+R)}{R}}=\dfrac{E}{\dfrac{r}{R}+1}$
When a resistance of infinity, let the voltage across the resistance be ${{V}_{1}}$ and the balancing length be ${{l}_{1}}$.
Therefore, ${{V}_{1}}=k{{l}_{1}}$ …. (i).
And ${{V}_{1}}=\dfrac{E}{\dfrac{r}{R}+1}$.
But, if $R\to \infty $ then $\dfrac{r}{R}\to 0$.
$\Rightarrow {{V}_{1}}=\dfrac{E}{0+1}=E$ …. (ii).
Let the voltage across the shunted resistance of 9.5$\Omega $ be ${{V}_{2}}$ and the balancing length be ${{l}_{2}}$.
Therefore, ${{V}_{2}}=k{{l}_{2}}$ …. (iii).
And ${{V}_{2}}=\dfrac{9.5E}{(r+9.5)}$ ….. (iv).
Divide equations (i) and (iii).
$\Rightarrow \dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{{{l}_{1}}}{{{l}_{2}}}$.
Here, ${{l}_{1}}$= 3cm and ${{l}_{2}}$= 2.85cm.
This gives us that
$\dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{3}{2.85}$.
Now, divide equations (ii) and (iv).
$\dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{E}{\dfrac{9.5E}{(r+9.5)}}=\dfrac{(r+9.5)}{9.5}$
But $\dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{3}{2.85}$.
Therefore,
$\dfrac{(r+9.5)}{9.5}=\dfrac{3}{2.85}$
$\Rightarrow 2.85(r+9.5)=3(9.5)$
$\Rightarrow 2.85r+27.075=28.5$
$\Rightarrow r=\dfrac{28.5-27.075}{2.85}=\dfrac{1.425}{2.85}=0.5\Omega $
Therefore, the internal resistance of the given cell is $0.5\Omega $
Hence, the correct option is C.
Note: Note that the emf of the unknown cell must always be less than the emf of the main cell. If the emf of the cell that is to be measured is more than the emf of the main cell, then the balancing length will be more than the length of the resistance wire and we will not be able to measure the emf of the cell.
Recently Updated Pages
10 Examples of Evaporation in Daily Life with Explanations

10 Examples of Diffusion in Everyday Life

1 g of dry green algae absorb 47 times 10 3 moles of class 11 chemistry CBSE

What is the meaning of celestial class 10 social science CBSE

What causes groundwater depletion How can it be re class 10 chemistry CBSE

Under which different types can the following changes class 10 physics CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which are the Top 10 Largest Countries of the World?

How do you graph the function fx 4x class 9 maths CBSE

Who was the leader of the Bolshevik Party A Leon Trotsky class 9 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Which is the largest saltwater lake in India A Chilika class 8 social science CBSE

Ghatikas during the period of Satavahanas were aHospitals class 6 social science CBSE




