Question

What is a projectile? Derive an equation of the path of a projectile.

Answer 1

Hint: First we need to draw the complete diagram for projectile motion showing all the forces, angles, distance, and everything that’s required. Now we know that there are three equations of motions, we have to derive the formula for the equation of the path of a projectile from that formula by changing certain values in it.

Complete step-by-step solution:
We know that, When a body is thrown with a certain velocity making some angle with horizontal, the path it follows is a parabolic trajectory called projectile.
We also know that the flight time of the projectile motion is the time taken for the object thrown at the projectile to the time when it reaches the surface again.

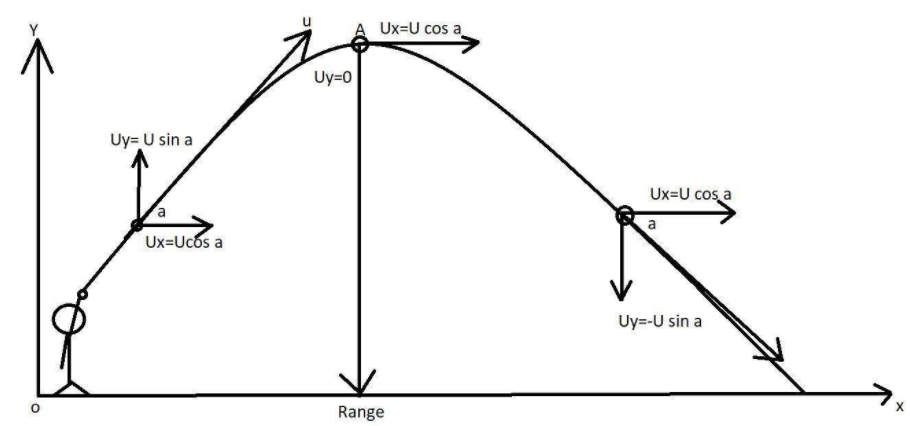
In the above diagram we see a boy throwing a ball at a certain angle ‘a’ and after that the forces working on that ball over some certain position and time. At point A the ball reaches the maximum height.

The point O is known as the point of projection.
In every position of the object, we will have to take the horizontal and vertical projection.
‘a’ is the angle of projection.
Here x = V cos at, as ‘cos at’ is the horizontal component.
We see that the vertical component taken in the first case is U sin a, and the horizontal component is U cos a.
Now, In the second case, the body does not have any vertical component as the velocity is reduced to zero, therefore the horizontal component is U cos a.
We can see in the third case, the body is not falling, so the vertical component acting downwards is -U sin a, and the horizontal component is U Cos a.
We must know that the total time that is taken by the object that is projected to the time it reaches the ground again and touches the surface is known as time of flight or flight time.

Now, For finding different values related to projectile motion, we can make use of the differential equations of motion.
Those are,
$v=u-gt$
$s=ut+\dfrac{1}{2}g{{t}^{2}}$
${{v}^{2}}={{u}^{2}}-2gs$ ,
Here we can see that, v is the final velocity, u is the initial velocity, g is the acceleration due to gravity, s is the distance traveled, t is the time taken.
Therefore we can say that the time of flight is, the resultant displacement in vertical motion is S=0.
$g{{t}^{2}}=2(uyt-sy)$ [here uy=u sin a and sy=0).
Therefore the total time of flight is,
$t=\dfrac{2u\sin a}{g}$ , by analysing these formulas, we can figure out various values from these formulas like horizontal range, maximum height but here in the question it is asked to derive the equation for the path of the projectile so,
Now, let us consider the position of the ball at any instant be P(x,y), now
$X=v\sin a \times t$.
$Y=v\sin a \times t-\dfrac{g{{t}^{2}}}{2}$.
Now on substituting equation 1 and 2 we get,
The equation of trajectory is:
$y=\dfrac{x\tan a-g{{x}^{2}}}{2{{u}^{2}}{{\cos }^{2}}a}$

Note: We are considering a variable position for the ball at any instance because then only we can say that the equation works at any place in the trajectory path of the object. In this case, the only acceleration working is the acceleration due to gravity hence the ‘a’ in the formula of motion changes to ‘g’.