Question

A proton and an $\alpha $- particle, accelerated through the same potential difference, enter a region of uniform magnetic field normally. If the radius of the proton orbit is 10cm, the radius of $\alpha $- particle.

A. $10cm$
B. $10\sqrt 2 cm$
C. $20cm$
D. $5\sqrt 2 cm$

Answer 1

Hint:The concept of Lorentz force must be applied to solve this problem. The Lorentz force is the combined force that a charged particle experiences when it enters a region of electric and magnetic field aligned perpendicular to each other.
Lorentz Force, $L = {F_E} + {F_B}$
where ${F_E}\& {F_B}$ are the forces due to electric field E and magnetic field B respectively.

Complete step-by-step answer:
Consider the following region of space with mutually perpendicular electric field, E and magnetic field, B. The direction of electric field is from left to right and the direction of magnetic field is into the plane of paper.

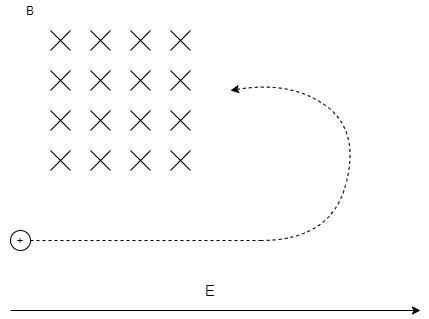
Consider a particle of charge +q that is entering the region as shown.
When it enters, it experiences combined force due to an electric and magnetic field, known as Lorentz force.
$L = {F_E} + {F_B}$
Electric field, ${F_E} = qE$ This force is along the direction of the electric field.

Magnetic field, ${F_B} = q\left( {\overrightarrow v \times \overrightarrow B } \right)$ where v = velocity.
Since, there is a cross-product of velocity and magnetic field, the force will be at the perpendicular direction as that of the magnetic field.
Thus, when the combined force acts on the particle, the particle experiences a force pushing it to move upwards. However, it cannot move upwards because the resultant force acting on the particle makes it hover around in circles with the magnetic force, ${F_B}$ providing the necessary centripetal force to the rotation.
The radius of rotation,
$r = \dfrac{{mv}}{{Bq}}$
Also, $v = \dfrac{{rBq}}{m}$
And $mv = rBq$
where m and v are the mass and the velocity of the particles, respectively.
We should, also, take into consideration that there is an electric field acting on the particle.
When the charge moves in the electric field, there is work done due to the force applied. This work done, translates into kinetic energy of the charge in the electric field which is equal to the potential energy of the charge inside the electric field.
$\dfrac{1}{2}m{v^2} = qV$
where V is the electric potential
$\dfrac{1}{2}m{v^2} = qV$
$ \Rightarrow \dfrac{1}{2}\left( {mv} \right)v = qV$

Substituting the values of mv and v from the above, we get –
$\dfrac{1}{2}\left( {rBq} \right)\dfrac{{rBq}}{m} = qV$
$\Rightarrow {r^2}{B^2}{q^2} = 2mqV$
     \[\Rightarrow {r^2} = \dfrac{{2mqV}}{{{B^2}{q^2}}}\]
     \[\Rightarrow {r^2} = \dfrac{{2mV}}{{{B^2}q}}\]
From the above equation, we can infer that –
${r^2} \propto \dfrac{m}{q}$
Or,
$r \propto \sqrt {\dfrac{m}{q}} $
The $\alpha $- particle is the nucleus of the helium atom which has 2 protons and 2 neutrons. Thus,
Mass of $\alpha $- particle, ${m_a} = 4{m_p}$ Charge of $\alpha $- particle, ${q_a} = 2{q_p}$
By taking the ratio,
$\dfrac{{{r_a}}}{{{r_p}}} = \dfrac{{\sqrt {\dfrac{{{m_a}}}{{{q_a}}}} }}{{\sqrt {\dfrac{{{m_p}}}{{{q_p}}}} }}$
$\Rightarrow \dfrac{{{r_a}}}{{{r_p}}} = \sqrt {\dfrac{{{m_a}}}{{{m_p}}} \times \dfrac{{{q_p}}}{{{q_a}}}}$
Substituting, we get –
$ \Rightarrow \dfrac{{{r_a}}}{{{r_p}}} = \sqrt {\dfrac{{4{m_p}}}{{{m_p}}} \times \dfrac{{{q_p}}}{{2{q_p}}}} = \sqrt 2 $
Since given, ${r_p} = 10cm$
Radius traced by the $\alpha $- particle , ${r_a} = 10\sqrt 2 cm$

The correct option is Option B.

Note:The direction of force induced on the armature is given by Fleming's Left-Hand rule.

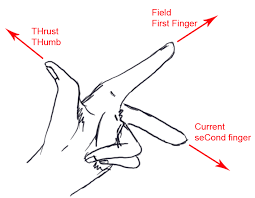
It says that if the left hand is held out as shown in the figure, by orienting the middle finger in the direction of electric field and the index finger in the direction of the magnetic field, we will be able to observe the direction of force acting on the conductor which is the same as the direction pointed by the thumb.