Question

What is a Pythagorean Triplet? Give some examples.

Answer 1

Hint: To understand the term ‘Pythagorean triplet’ we will consider a right angle triangle. Now, we will take some examples of the cases where we will assign some positive integers as the lengths of the base and the perpendicular and use the Pythagoras theorem to find the length of the hypotenuse. If they turn out to be an integer then the triplet will be known as the Pythagorean triplet otherwise not.

Complete step by step solution:
Here we have been asked about the term ‘Pythagorean Triplet’. To understand this term we need to consider a right angle triangle, so let us draw a right angle triangle.

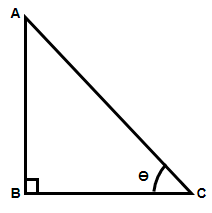
Now, here we can say that AB is the perpendicular (P), BC is the base (B) and AC is the hypotenuse (H) as per the convention. So, a Pythagorean Triplet is defined as the set of three positive integers that satisfies the Pythagoras theorem given as ${{H}^{2}}={{P}^{2}}+{{B}^{2}}$. In case any of the sides is not an integer even after satisfying the theorem then that triplet is not called the Pythagorean Triplet. Let us take a few examples.
(i) Consider the length of the base BC as 3 cm and the length of the perpendicular AB as 4 cm, so using the Pythagoras theorem we get,
$\begin{align}
  & \Rightarrow A{{C}^{2}}={{4}^{2}}+{{3}^{2}} \\
 & \Rightarrow A{{C}^{2}}=25 \\
 & \Rightarrow AC=5cm \\
\end{align}$
Clearly 3 cm, 4 cm and 5 cm is a Pythagorean Triplet.
(ii) Consider the length of the base BC as 6 cm and the length of the perpendicular AB as 8 cm, so using the Pythagoras theorem we get,
$\begin{align}
  & \Rightarrow A{{C}^{2}}={{8}^{2}}+{{6}^{2}} \\
 & \Rightarrow A{{C}^{2}}=100 \\
 & \Rightarrow AC=10cm \\
\end{align}$
Clearly 6 cm, 8 cm and 10 cm is a Pythagorean Triplet.
(iii) Consider the length of the base BC as 12 cm and the length of the perpendicular AB as 5 cm, so using the Pythagoras theorem we get,
$\begin{align}
  & \Rightarrow A{{C}^{2}}={{5}^{2}}+{{12}^{2}} \\
 & \Rightarrow A{{C}^{2}}=169 \\
 & \Rightarrow AC=13cm \\
\end{align}$
Clearly 5 cm, 12 cm and 13 cm is a Pythagorean Triplet.
(iv) Consider the length of the base BC as 10 cm and the length of the perpendicular AB as 5 cm, so using the Pythagoras theorem we get,
$\begin{align}
  & \Rightarrow A{{C}^{2}}={{10}^{2}}+{{5}^{2}} \\
 & \Rightarrow A{{C}^{2}}=125 \\
 & \Rightarrow AC=5\sqrt{5}cm \\
\end{align}$
Since $5\sqrt{5}$ is not an integer so we can say that 5 cm, 10 cm and $5\sqrt{5}cm$ is not a Pythagorean Triplet.

Note: Remember the basic terms used in the above solution. Note that there are infinite Pythagorean triplets so you can take many examples. Even if we know the length of one side of a right triangle and one of the angles other than the 90 degrees then we can determine the measure of all the sides using trigonometry.