Question

A quadratic polynomial has no zero. Its graph…..
A) Touches X-axis at any point
B) Intersects X-axis at two distinct points
C) Does not intersect X-axis at any points
D) Is in any half-plane of the X-axis.

Answer 1

Hint: A quadratic polynomial is a polynomial of degree 2. An equation involving a quadratic polynomial is a quadratic equation. The standard form is
 \[a{{x}^{2}}+bx+c=0\]
with a, b, and c being constants or numerical coefficients, and x is an unknown variable. One absolute rule is that the first constant "a" cannot be a zero.

Complete step-by-step solution:
The x-intercepts are the points at which the parabola crosses the x-axis. If they exist, the x-intercepts represent the zeros, or roots, of the quadratic function.
Now, in the question, it is mentioned that a given quadratic polynomial has no zero.
Let us assume that the quadratic polynomial is the form
\[p{{x}^{2}}+qx+r=0\]
We also know that the roots of the above quadratic polynomial are
X= \[\dfrac{-q+\sqrt{{{q}^{2}}-4pr}}{2p},\dfrac{-q-\sqrt{{{q}^{2}}-4pr}}{2p}\]
We also know that for a quadratic equation if x-intercept exist it means that the given equation has roots or also it can be concluded that the graph of the polynomial crosses the x- axis.
But, from our question, it is said that the quadratic polynomial has no zero, which means there exists no x for which the graph intersects the x-axis.
In the diagram below we can see an example of a parabola which is the graph of a quadratic polynomial, it is given in the question that it doesn’t have a zero which implies that the quadratic equation had no roots and hence it doesn’t intersect the x-axis. As the roots of the polynomial lie on the x-axis.

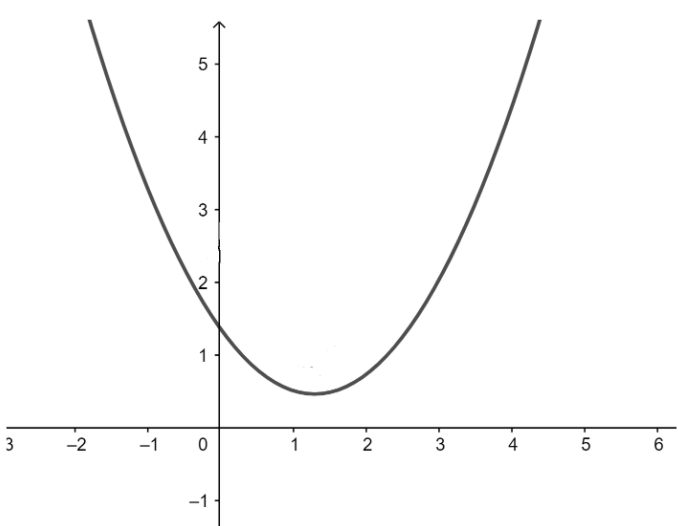
In the diagram below the parabola touches the x-axis, from which we can conclude that the parabola would have two equal roots.

In option A it is given that the graph touches the x-axis at one point, which would be false because if the graph intersects the x-axis at one point then y=0 will be zero for some x.
Hence option C is correct which is the graph doesn’t intersect the x-axis at any point.

Note: Students should read the question properly or they might get confused with what is actually given. A quadratic polynomial has at most two real roots so the maximum no of times the graph will intersect the x-axis is two and the minimum would be zero when the equation has no roots.