Question

A quadrilateral whose diagonals are equal and bisect each other at right angles is called a:
\[
  \left( a \right){\text{Rhombus}} \\
  \left( b \right){\text{Square}} \\
  \left( c \right){\text{Rectangle}} \\
  \left( d \right){\text{Trapezium}} \\
 \]

Answer 1

Hint: In this question, we have to use the given property of quadrilateral and then prove any unique property of quadrilateral. So, we can easily identify the correct option.

Complete step-by-step answer:

Let us consider a quadrilateral ABCD in which the diagonals AC and BD intersect each other at o.

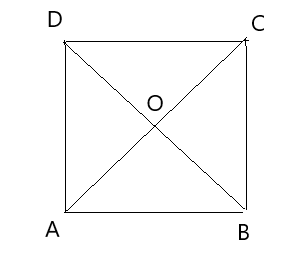
Given, the diagonals of ABCD are equal and bisect each other at right angles.

Therefore, AC = BD, OA = OC, OB = OD, and $\angle AOB = \angle BOC = \angle COD = \angle AOD = {90^0}$

Now, In $\vartriangle AOB$ and $\vartriangle COD$
AO = CO (Diagonals bisect each other)
OB = OD (Diagonals bisect each other)
$\angle AOB = \angle COD = {90^0}$ (Vertically opposite angles)
So, $\vartriangle AOB \cong \vartriangle COD$ (SAS congruence rule)
Hence AB = CD (By CPCT) ...........(1)
And, $\angle OAB = \angle OCD$ (By CPCT)

However, these are alternate interior angles for line AB and CD and alternate interior angles are equal to each other only when the two lines are parallel.

So, $AB\parallel CD............\left( 2 \right)$
From (1) and (2) equation,
ABCD is a parallelogram.

In $\vartriangle AOD$ and $\vartriangle COD$
AO = CO (Diagonals bisect each other)
OD = OD (Common)
$\angle AOD = \angle COD = {90^0}$
So, $\vartriangle AOD \cong \vartriangle COD$ (SAS congruence rule)
Hence AD = DC ……….. (3)

However, AD = BC and AB = CD (Opposite sides of parallelogram ABCD)
So, AB = BC = CD = DA

Therefore, all the sides of quadrilateral ABCD are equal to each other.
In $\vartriangle ADC$ and $\vartriangle BCD$
AD = BC (Already proved)
AC = BD (Given)
CD = CD (Common)

So, $\vartriangle ADC \cong \vartriangle BCD$ (SSS Congruence rule)
Hence, $\angle ADC = \angle BCD$ (By CPCT)

However, $\angle ADC + \angle BCD = {180^0}$ (Co-interior angles)
$
   \Rightarrow \angle ADC + \angle ADC = {180^0} \\
   \Rightarrow 2\angle ADC = {180^0} \\
   \Rightarrow \angle ADC = {90^0} \\
 $
One of the interior angles of quadrilateral ABCD is a right angle.

Thus, we have obtained that ABCD is a parallelogram, AB = BC = CD = AD and one of its interior angles is ${90^0} \\$ . Therefore, ABCD is a square.

So, the correct option is (b).

Note: Whenever we face such types of problems we use some important points. Like first we prove that quadrilateral ABCD is a parallelogram and all sides of quadrilateral are equal then prove one of the interior angles of quadrilateral ABCD is a right angle. So, according to this property it is proved that the quadrilateral is Square.