Question

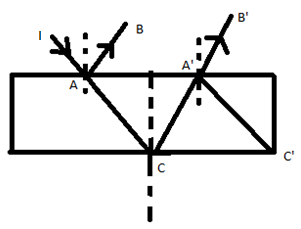
A ray of light intensity $I$ is incident on a parallel glass slab and refraction. At each reflection, $25\% $ of incident energy is reflected. The rays $AB$ and $A'B'$ undergo interference. The ratio of ${I_{max}}$ and ${I_{\min }}$ is

A. $49:1$
B. $7:1$
C. $4:1$
D. $8:1$

Answer 1

Hint:
Here first we have to find the value of $AB$ and $A'B'$ and then the ratio of $AB$ and $A'B'$ .At last we have to find the ratio of ${I_{max}}$ and ${I_{\min }}$

Complete step by step solution:
Given,
A ray of light intensity $I$ is incident on a parallel glass slab and refraction.
At each reflection, $25\% $ of incident energy is reflected.
The rays $AB$ and $A'B'$ undergo interference.
Since, $I$ is incident on a parallel glass slab and $25\% $ incident energy is reflected.
So, $AB = \dfrac{I}{4}$
$
AC = (100 - 25)\% \times I \\
 = 75\% \times I \\
 = \dfrac{{3I}}{4}
$
$
A'C = 75\% \times 25\% I \\
= \dfrac{{3I}}{{16}}
$
$
A'B' = 75\% \times 25\% \times 75\% I \\
= \dfrac{{9I}}{{64}}
$
Now let ${I_1} = \dfrac{I}{4}$ and ${I_2} = \dfrac{{9I}}{{64}}$
Now let us find the ratio of ${I_{max}}$ and ${I_{\min }}$
$
\Rightarrow \dfrac{{{I_{\max }}}}{{{I_{\min }}}} = {\left( {\dfrac{{\sqrt {\dfrac{{{I_2}}}{{{I_1}}}} + 1}}{{\sqrt {\dfrac{{{I_2}}}{{{I_1}}}} - 1}}} \right)^2} \\
\Rightarrow \dfrac{{{I_{\max }}}}{{{I_{\min }}}} = {\left( {\dfrac{{\sqrt {\dfrac{9}{{16}}} + 1}}{{\sqrt {\dfrac{9}{{16}}} - 1}}} \right)^2} \\
\Rightarrow \dfrac{{{I_{\max }}}}{{{I_{\min }}}} = \dfrac{{49}}{1}
$
So, the ratio of ${I_{max}}$ and ${I_{\min }}$ is $\dfrac{{49}}{1}$

Hence, option A is correct.

Additional information:
Total internal reflection and critical angle- In optics total internal reflection is the complete reflection of a beam of light in a medium such as water or glass back onto the medium from the surrounding surfaces. If the angle of incidence is greater than a certain limiting angle, called the critical angle, the phenomenon of total internal reflection occurs.
Reflection on a glass slab- As light penetrates the glass slab through air, they are refracted and bend towards the normal. The path of the refracted ray now shifts again as it comes into the air from the glass plate. If the beam of light passes from a denser to a rarer medium, it bends away from the normal.

Note:
Here we have to keep in mind that at each reflection, $25\% $ incident energy is reflected. So, the value of each incident ray will be different. Also for the formula of $\dfrac{{{I_{\max }}}}{{{I_{\min }}}} = \left( {\dfrac{{\sqrt {\dfrac{{{I_2}}}{{{I_1}}}} + 1}}{{\sqrt {\dfrac{{{I_2}}}
{{{I_1}}}} - 1}}} \right)$, we cannot swap the numerator and denominator in confusion. So, we have to be very careful while solving this.