Question

A ray of light is incident at $ 60^\circ $ on a prism of refracting angle $ 30^\circ $ . The emerging ray is at an angle $ 30^\circ $ with the incident ray. The value of the refractive index of the prism is?
(A) $ \dfrac{{\sqrt 3 }}{4} $
(B) $ \dfrac{{\sqrt 3 }}{2} $
(C) $ \sqrt 3 $
(D) $ \dfrac{2}{{\sqrt 3 }} $

Answer 1

Hint :In this question, we have to use the concept of refraction of light when it passes through a prism. The refractive index is a measure of comparing different materials. It tells how fast light can travel through a medium. Since $ {\delta _m} $ is not given so we cannot use the formula $ \mu = \dfrac{{\sin (A + \dfrac{{{\delta _m}}}{2})}}{{\sin (\dfrac{A}{2})}} $ . Instead find $ {r_1} $ and use the formula $ \mu = \dfrac{{\sin {i_1}}}{{\sin {r_1}}} $ , since $ {i_1} $ is given.

Complete Step By Step Answer:
Given are the following information: Incident angle $ {i_1} = 60^\circ $ , Angle of prism $ A = 30^\circ $ , Angle of deviation(angle between incident ray and emergent ray) $ \delta = 30^\circ $ . Let the emergent angle be $ {i_2} $ , refractive angle at incident plane $ {r_1} $ and refractive angle at emergent plane $ {r_2} $ as shown in the figure-

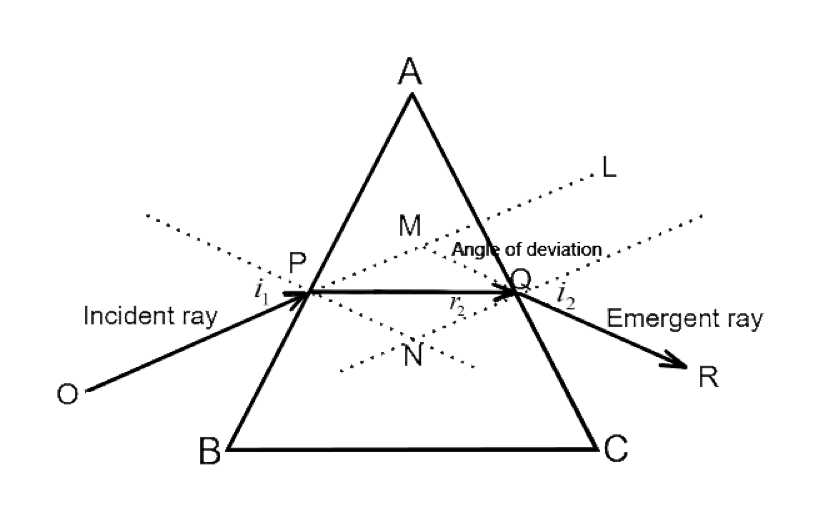
From the figure we note that $ {i_1} = {r_1} + {\delta _1} $ and $ {i_2} = {r_2} + {\delta _2} $ . Adding both equations we have
 $ {i_1} + {i_2} = {r_1} + {r_2} + {\delta _1} + {\delta _2} $ (1)
 From $ \vartriangle PMQ $ and $ \square APNA $ we see that $ \delta = {\delta _1} + {\delta _2} $ and $ A = {r_1} + {r_2} $ respectively
Substituting this and respective values of variables in equation 1, we get,
 $ {i_1} + {i_2} = A + \delta \Rightarrow {i_2} = 0^\circ $
 which further implies that
  $ {r_2} = 0^\circ \Rightarrow {r_1} = A = 30^\circ $
Using Snell’s law $ \mu = \dfrac{{\sin {i_1}}}{{\sin {r_1}}} \Rightarrow \mu = \dfrac{{\sin 60^\circ }}{{\sin 30^\circ }} \Rightarrow \mu = \sqrt 3 $
Therefore, the refractive index of the prism $ \mu = \sqrt 3 $ .
The answer is option (C).

Note :
Don’t get confused by the term refracting angle. It is not the refractive angle at the incident plane. The angle of prism A is also called refracting angle. Also, whenever it is mentioned the angle made by emergent ray with incident ray it means the total deviation $ \delta ( = {\delta _1} + {\delta _2}) $ .