Question

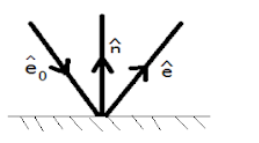
A ray of light is reflected by a plane mirror. $ {e_0} $ ​, $ e $ and $ n $ be the unit vectors along the incident ray, reflected ray and the normal to the reflecting surface respectively. Which of the
following gives an expression for $ e $ ?

 $ \left( A \right)\widehat {{e_0}} - 2\left( {\widehat {{e_0}} \cdot \widehat n} \right)\widehat n \\
  \left( B \right)\widehat {{e_0}} + 2\left( {\widehat {{e_0}} \cdot \widehat n} \right)\widehat n \\
  \left( C \right)\widehat {{e_0}} - \left( {\widehat {{e_0}} \cdot \widehat n} \right)\widehat n \\
  \left( D \right)\widehat {{e_0}} + \left( {\widehat {{e_0}} \cdot \widehat n} \right)\widehat n \\ $

Answer 1

Hint : In order to solve this question, we are first of all going to compute the dot products of the vectors $ {e_0} $ and $ n $ , the vectors $ e $ and $ n $ , after that the former is subtracted from the latter and the relation which is obtained is further simplified according to the options given and the correct option is chosen.
The dot product of two unit vectors $ e $ and $ n $ having angle $ \theta $ between them is given by
 $ e \cdot n = 1 \times 1 \times \cos \theta \\
   \Rightarrow e \cdot n = \cos \theta \\ $
And if the vectors are in opposite direction, the angle taken between them is $ 180 - \theta $

Complete Step By Step Answer:
Let us consider that the angles between the vectors $ {e_0} $ ​and $ e $ ,
 $ e $ and $ n $ be $ \theta $ each
This implies that the dot product of the vectors $ {e_0} $ and $ n $ will be
 $ {e_0} \cdot n = 1 \times 1\cos \left( {180 - \theta } \right) \\
   \Rightarrow {e_0} \cdot n = - \cos \theta \\ $
And the dot product for the unit vectors $ e $ and $ n $ will be
 $ e \cdot n = 1 \times 1 \times \cos \theta \\
   \Rightarrow e \cdot n = \cos \theta \\ $
Subtracting the above two cross products
We get
 $ e \cdot n - {e_0} \cdot n = \cos \theta + \cos \theta = 2\cos \theta $
Further solving this expression, we get
 $ n\left( {e - {e_0}} \right) = 2\cos \theta \\
  n\left( {e - {e_0}} \right) = 2\left[ { - {e_0} \cdot n} \right] \\ $
Doing dot product with $ n $ on both the side
 $ n\left( {e - {e_0}} \right) \cdot n = 2\left[ { - {e_0} \cdot n} \right] \cdot n \\
   \Rightarrow e = {e_0} - 2\left( {{e_0} \cdot n} \right) \cdot n \\ $
So, option $ \left( A \right) $ is correct.

Note :
It is important to note that as the unit vectors are from the incident and reflected rays from a mirror, so they form equal angles with the normal, this fact has been used with much importance in this question. As the directions of the $ {e_0} $ and $ n $ vectors are opposite that is why the angle between them is taken as $ 180 - \theta $ .