Question

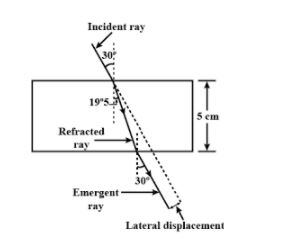
A ray of light strikes a glass slab 5 cm thick, making an angle of incidence equal to 30°. Construct the ray diagram showing the emergent ray and the refracted ray through the glass block. The refractive index of glass is 1.5. Also, measure the lateral displacement of the ray. Take $\sin{19.5°=\ \dfrac {1}{3}}$.

Answer 1

Hint: Use Snell’s Law to find angle of refracted ray. Then by substituting the values in the formula for lateral displacement calculate lateral displacement. And finally using all these data draw the ray diagram showing emergent ray and refracted ray through the glass block.

Formula used:
$\mu = \dfrac{\sin{i}}{\sin{r}}$
$Lateral\ Displacement= t \times \dfrac {\sin {(i-r)} }{\cos {r} }$

Complete step-by-step answer:
Given: Thickness (t)= 5cm
             Refractive Index ($\mu$) =1.5
             Angle of incidence= 30°
We know Snell’s Law is given as,
$\mu = \dfrac{\sin{i}}{\sin{r}}$
Rearranging the above equation we get,
$sinr = \dfrac{\sin{i}}{\mu}$
Now by substituting the given values we get,
$sinr = \dfrac{\sin{30°}}{1.5}$
$sinr=\dfrac {\dfrac {1}{2} }{1.5}$
$\therefore sinr=\dfrac {1}{3}$
$\therefore \ r=\arcsin {\dfrac {1}{3} }$
$\therefore \ r= 19.5°$
Now to calculate lateral displacement, the formula is given by,
$Lateral\ Displacement= t \times \dfrac {\sin {(i-r)} }{\cos {r} }$
Substituting the values we get,
$\therefore Lateral\ Displacement= 5\times \dfrac {\sin {(30°-19.5°)} }{\cos {19.5°} }$
$\therefore Lateral\ Displacement= 5\times \dfrac {\sin {(10.5°)} }{\cos {19.5°} }$
$\therefore Lateral\ Displacement=0.97$
Hence, the lateral displacement of the ray is 0.97cm.

Note: There’s an alternate formula to calculate lateral displacement you can use that as well. The alternate formula is given by,
$Lateral\ Displacement= t \times i\left( 1 - \dfrac {r}{i} \right)$