Question

A rectangle has a perimeter 72m. If its length is thrice of its breadth. Find breadth.

Answer 1

Hint: The formula of calculating the perimeter of the rectangle is just the sum of all sides, as opposite sides of the rectangle are equal, so we just write two times the sum of adjacent sides. Just put the value of length in the formula of perimeter and you will be able to calculate the breadth from the linear equation formed.

Complete step-by-step answer:
Now to find the breadth of the rectangle we need two things first is the value of perimeter and the second is value of length or in this case length in terms of breadth because we have only one equation and we have two variables length and breadth which we have to find but we have length in terms of breadth which is,

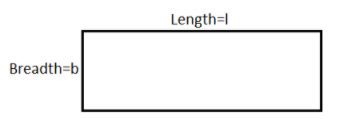
Let length of rectangle be l and breadth be b, and perimeter be P,
\[l=3b\]

The formula to find the perimeter of rectangle is,
\[P=2(l+b)\]
Putting the value of l in equation of P, we get,
\[P=2(3b+b)\]
\[\begin{align}
  & P=2(4b) \\
 & P=8b \\
\end{align}\]
Now put the value of perimeter given in the question,
\[\begin{align}
  & 72=8b \\
 & b=\dfrac{72}{8}=9 \\
\end{align}\]

The value of breadth is 9m.

Note: Important point is that the number of variables whose values has to be found should be equal to the number of equations only then it will be feasible for us to proceed with the solution of the question. If the number of equations is less than the number of variables then it will not be possible to solve the question but the opposite situation can turn out to be useful. Do not forget to mention the units all along the way because if you miss then your marks will be deducted. In the case of area you can end up with a quadratic equation and then find the roots of that equation using quadratic formula and then select one value which will satisfy all the conditions of the question.