Question

A rectangle is symmetrical about the lines joining the ---- of the opposite sides \[\]
A. midpoints \[\]
B. vertices \[\]
C. points \[\]
D. none of the above \[\]

Answer 1

Hint: We join the two points as given in each option of the question and check whether line joining the two points acts as a line of symmetry for the two points. We do that by checking whether the distance of the two points from the line is equal or not.

Complete step-by-step solution:
We know that a geometric shape or object is symmetric if it can be divided into two or more identical pieces that are arranged in an organized fashion. The line of symmetry is a type of reflection of symmetry where a line divides the shape into two parts which are reflecting mirror images of each other. We shall check the symmetrize of a rectangle by joining the points given in each option.
Checking option-A: Let us observe any rectangle ABCD. We take the midpoints of AB as P and midpoint of CD as Q. We join PQ. \[\]
 

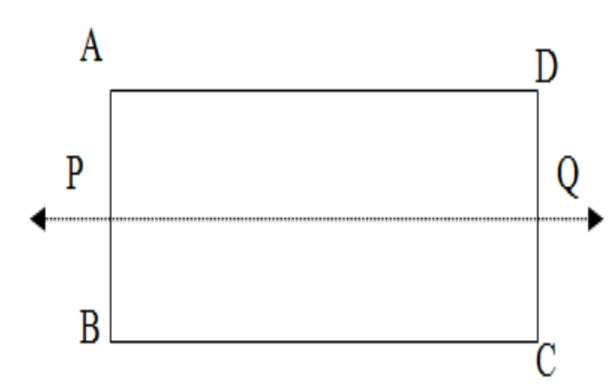
We observe here the line PQ acts as a mirror, which reflects point A to B as well as point B to A(AP=PB). Similarly, PQ also reflects D to C and C to D(CQ=DQ). So the line PQ is a line of symmetry. We can also join the midpoint of AD say R and the midpoint of BC say S and find the line of symmetry RS which makes the pair of points A, D, and B, C mirror images of each other. \[\]

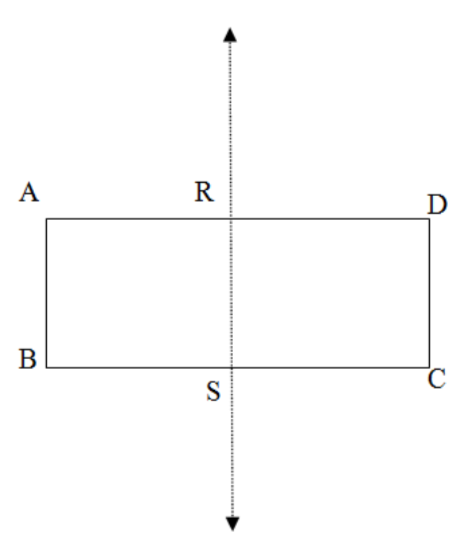
So we get two lines about which the rectangle is symmetrical. So option A is correct.
Checking Option-B: We join any 2 vertices say A and C of the opposite side. We take points to say P and Q on the opposite side of AC such that PQ is perpendicular to AC and join them. The point of intersection of AB and PQ is said X. \[\]

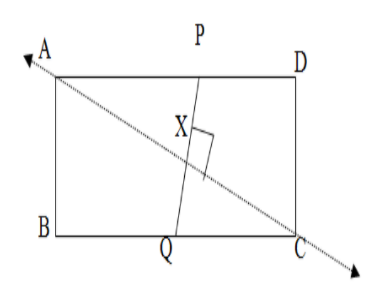
We observe that the lengths of PX and QX are not equal. So the diagonal AC cannot be a line of symmetry for the rectangle ABCD. We can similarly join BD and find that BD also cannot be a line of symmetry. So option B is not correct. \[\]
Checking Option-C: Let P be any point on AB and Q be any point( both P and Q should not be midpoints at the same time ) on the opposite side of AB that is the CD. We join PQ and two points R ad S on the rectangle on the opposite sides AD and BC such that RS is perpendicular to PQ. Let the point of intersection of PQ and RS be X. \[\]

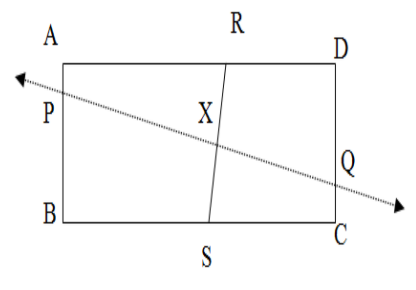
We observe that the lengths of RX and SX are not equal. So the line PQ cannot be a line of symmetry for the rectangle ABCD. We can similarly take P on AD and Q on BC and find PQ cannot be a line of symmetry. So option C is not correct. So the only correct option is A.

Note: A reflection of symmetry is about a point in one dimension, about a line in two dimensions, and a plane in three dimensions. The medians in an equilateral triangle are also lines of symmetry. The other types of symmetries are rotational, translational, and helical. If a shape is not symmetric it is asymmetric.