
A rectangular block of wood has dimensions 24 cm by 8 cm by 7 cm. It is cut up into children’s bricks. Each brick is a cube of side 3 cm. Find the volume of the wood that is left.
Answer
501k+ views
1 likes
Hint: We are given the dimensions of a cuboid wooden box. So, we use L = 24, B = 7 and H = 8 to find the volume of the total wood using the formula of volume of a cuboid,
Complete step by step answer: We are given that the rectangular block of the wood has dimensions 24 cm by 8 cm by 7 cm.
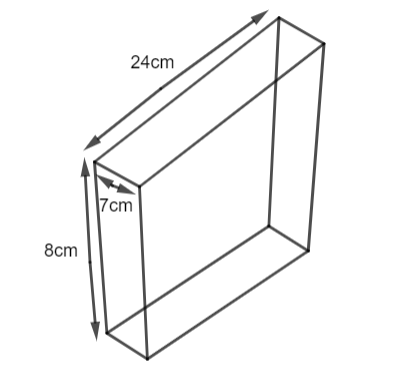
First, we will find the volume of the rectangular block. We know that the volume of the cuboid is given as
We have, L = 24, B = 7 and H = 8. So, we get,
So, we get the total volume of the wooden block as
Now, we know that out of this, the small cubes are cut down. The dimension of the cube is
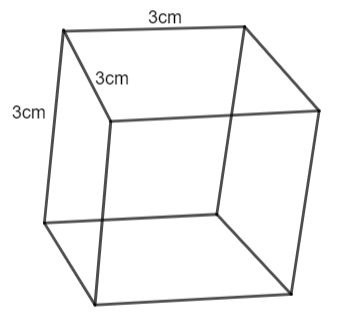
Now, we will find the volume of one cube and the volume is given as
Let us assume that the number of cubes that can be cut from the cuboid is n. So, we get,
Now using (i) and (ii), we get,
Now, divide both the sides by 27, we get,
Now, after the division, we see that 1344 is not completely divisible by 27.
When 1344 is divided by 27, it will give the remainder as 21 and quotient as 49. So, we get 49 cubes cut down and
Hence, the volume of the wood left is
Note: Another method to find the remaining is to just look at the remainder and another way is to subtract the total volume of the cube from the cuboid. As the quotient is 49 means 49 cubes are cut. So, the Total Volume of wood – Volume of the cube gives us the remaining wood. So,
So, we get,
Remaining Wood = 1344 – 1323 =
Complete step by step answer: We are given that the rectangular block of the wood has dimensions 24 cm by 8 cm by 7 cm.

First, we will find the volume of the rectangular block. We know that the volume of the cuboid is given as
We have, L = 24, B = 7 and H = 8. So, we get,
So, we get the total volume of the wooden block as
Now, we know that out of this, the small cubes are cut down. The dimension of the cube is

Now, we will find the volume of one cube and the volume is given as
Let us assume that the number of cubes that can be cut from the cuboid is n. So, we get,
Now using (i) and (ii), we get,
Now, divide both the sides by 27, we get,
Now, after the division, we see that 1344 is not completely divisible by 27.
When 1344 is divided by 27, it will give the remainder as 21 and quotient as 49. So, we get 49 cubes cut down and
Hence, the volume of the wood left is
Note: Another method to find the remaining is to just look at the remainder and another way is to subtract the total volume of the cube from the cuboid. As the quotient is 49 means 49 cubes are cut. So, the Total Volume of wood – Volume of the cube gives us the remaining wood. So,
So, we get,
Remaining Wood = 1344 – 1323 =
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




