Question

A rectangular garden 10m by 16m is to be surrounded by a concrete walk of uniform width. Given that the area of the walk is 120 square meters assuming the width of the walk to be x, form an equation in x and solve it to find the value of x?

Answer 1

Hint: We have been given the dimensions of the rectangular garden and hence we can determine its area using length x breadth. Now, we will consider the concrete path to have a width of x m throughout. So, new dimensions of garden and path together would be 16+2x and 10+2x. We also have the area of the concrete walk and therefore we can get the total area. To find out the width of the walk we can form an equation in x by equating (16+2x)(10+2x) to the total area calculated.

Complete step by step answer:
The following figure will give us better clarity.
Figure:

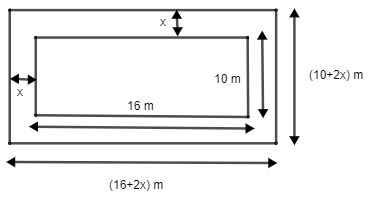
Let us start by calculating the area of the rectangular garden.
Length of the rectangular garden = 16 m
Breadth of the rectangular garden = 10 m
Area of the rectangular garden \[ = \,length \times \,breadth\]
 \[
   = \,16 \times 10 \\
   = \,160\,{m^2} \\
\]
We have already been given the area of the concrete walk as 120\[{m^2}\].
Now,
Let us calculate the total area of the rectangular garden and the sidewalk.
Total area= Area of rectangular garden + Area of the path
\[
   = \,160 + 120 \\
   = \,280\,{m^2} \\
\]
We will assume the uniform width of the sidewalk as x.
Now, in order to get an equation in terms of x, we will first get the expressions for the length and breadth of the total rectangular area in terms of x. We will get,
For length, we can see that the total length will be the sum of the length of the rectangular garden and the width x of the sidewalk on both sides.
Length of the whole rectangle (including concrete path) \[ = \left( {16 + 2x} \right)\,m\]
Similarly, we can see the breadth of the entire rectangle will be the sum of the breadth of the rectangular garden and the width x of the side walk on both sides. It will give us the expression as follows,
Breadth of the whole rectangle (including concrete path) \[ = \left( {10 + 2x} \right)m\]
We will use these expressions in the total area equation,
Area of the whole rectangle\[ = \] Length\[ \times \]Breadth
Now we will substitute the values of length and breadth which we calculated above in the area equation.
\[ \Rightarrow \left( {16 + 2x} \right)\left( {10 + 2x} \right) = 280\]
We will multiply the brackets and simplify the equation further,
\[
   \Rightarrow 4{x^2} + 52x + 160 = 280 \\
   \Rightarrow 4{x^2} + 52x + 160 - 280 = 0 \\
   \Rightarrow 4{x^2} + 52x - 120 = 0 \\
\]
To get the coefficient of \[{x^2}\]as 1, we will divide the entire equation by 4.
\[ \Rightarrow {x^2} + 13x - 30 = 0\]
We will split the middle term to get the roots of the above quadratic equation.
\[
   \Rightarrow {x^2} + 15x - 2x - 30 = 0 \\
   \Rightarrow x\left( {x + 15} \right) - 2\left( {x + 15} \right) = 0 \\
   \Rightarrow \left( {x - 2} \right)\left( {x + 15} \right) = 0 \\
\]
\[\therefore \,x = 2\,or\,x = - 15\]
We know that the width of the sidewalk cannot be negative.
So the value of x is 2.

Hence, the width of the sidewalk is 2 m.

Note: When forming the equation in x remember to consider the width on both sides of the length and breadth of the garden, i.e. add 2x instead of x. Also, while forming the quadratic equation keep in mind to keep it as simple as possible by making the coefficient of \[{x^2}\] as 1. Since, the variable x is nothing but the width of the sidewalk its value will always be positive, so we will always choose the positive root of the equation.