Question

A rectangular parallelopiped is formed by drawing planes through the points (-1,2,5) and (1,-1,-1) and parallel to the coordinate planes. The length of the diagonal of the parallelopiped is:
(a) 2
(b) 3
(c) 6
(d) 7

Answer 1

Hint: We know the diagonal of parallelopiped is the square root of the sum of squares of its edges. So, first we need their edge’s length. So, by that we can get the diagonal. First we have 2 points. All the planes pass through these points. So, the distance between these planes are edges. So the difference between corresponding coordinates, we get the edge lengths. Now the final sum of squares and then add them together.

Complete step-by-step solution -
Parallelopiped: In geometry, a parallelopiped or parallelopipedal is a three-dimensional figure by six parallelograms. By analogy it relates to a parallelogram just as a cube relates to a square.

Diagonal of Parallelopiped: As we know three sides a, b, c. The diagonal will be the square root of the sum of squares of these 3 edges of parallelopiped.
Diagonal= $\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}...........(i)$

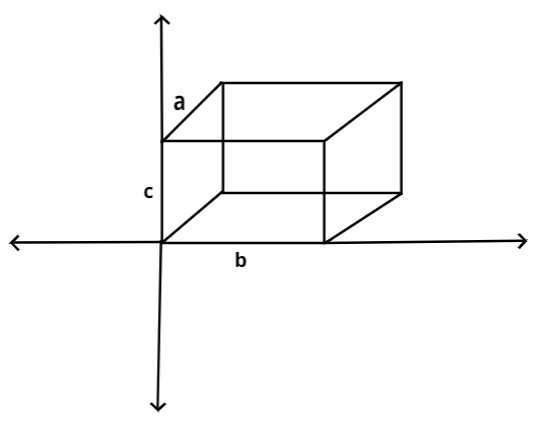
Given condition in the question, parallelopiped’s planes passes through (-1,2,5) (1,-1,-1).
So, all the planes pass through these points. Now the distance between planes through (a,0,0) (b,0,0) is b-a.
Similarly, we can generate 3 pairs of planes from each coordinate from these 2 points.
Let the first edge be assumed as a in the question.
We take ‘a’ as x-coordinates edge. So, by subtracting both x’s we get,
a=1-(-1)
By simplifying the above, we get value of a as:
a=2
by squaring on both sides, we get value of it as:
${{a}^{2}}=4......(ii)$
Let the second and third edges be b, c in this question we take “b” as distance between y- coordinates and “c” as distance between z- coordinates
So, by subtracting y-coordinate, we get the value of b as:
b= -1-2=-3
by subtracting z coordinates, we get the value of c as:
c=-1-5=-6
By squaring both the above equation we get their values as:
${{b}^{2}}=9........(iii);\,\,{{c}^{2}}=36.......(iv)$
By substituting equations (iii),(iv),(ii) in the equation (i), we get:
Diagonal = $\sqrt{4+9+36}$
by simplifying the root; we get its value as:
Diagonal =7
Therefore option (d) is correct for the given radius in the question.

Note: Be careful while stating analogy of planes, distance. So, when we find the plane's distance, the order of difference doesn’t matter because in the next step we square them. So, you may apply for an order. Don’t consider the negative root for diagonal because it’s a length it must always be greater than 0.