Question

A rectangular piece of paper is 100 cm $\times $ 44 cm. A cylinder is formed by rolling the paper along its length then the volume of the cylinder so formed is
(A). 15400 $c{{m}^{3}}$
(B). 15500 $c{{m}^{3}}$
(C). 15800 $c{{m}^{3}}$
(D). 15300 $c{{m}^{3}}$

Answer 1

Hint: A cylinder is nothing but a set of circular discs stacked one upon the other. So if you compute the space occupied by each of these discs and add them up, what we get is the volume of the cylinder.

Complete step-by-step solution -
When the rectangular piece of paper is rolled along its length, the length of the piece of paper forms the circumference of the base of the cylinder and breadth of paper forms the height of the cylinder.
Length of the rectangular piece of paper is 44 cm and width of the rectangular paper is 100 cm

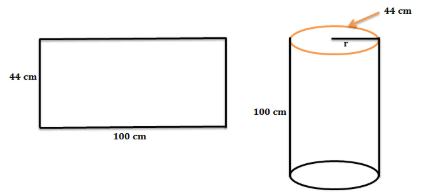
Let us say that the circular discs are stacked up to the height. Now, the volume of the cylinder will be the product of the base area of the discs and the height.
The whole length of the circular base = circumference of the circular base = 44 cm.
The circumference of the circular base $=2\pi r$
$44=2\pi r$
Dividing both sides by 2, we get
$22=\pi r$
Put the value of the $\pi =\dfrac{22}{7}$ , we get
$22=\dfrac{22}{7}(r)$
Dividing both sides by 2, we get
$1=\dfrac{1}{7}(r)$
$r=7$
The area of the circular base $=\pi {{r}^{2}}$
The area of the circular base $=\dfrac{22}{7}\times {{(7)}^{2}}=22\times 7=154$
Height of the cylinder = width of the rectangular paper = 100 cm.
The volume of the cylinder = $154\times 100=15400$ .
Hence the volume of the cylinder is 15400 $c{{m}^{3}}$.
Therefore, the correct option for the given question is option (a).

Note: Alternatively, you could substitute the radius and height of the cylinder directly into the formula for volume of the cylinder $\left( V=\pi {{r}^{2}}h \right)$. Sometimes students make mistakes in finding the radius; they directly put the length as the diameter of the base of the cylinder which is wrong so students needed to be careful.