
A rectangular water tank of base
Answer
490.5k+ views
Hint: We have been given the dimensions of the rectangular tank and the height of the water in it, which gives the volume of the water. So we will calculate the volume of water in the rectangular tank by using the formula
Complete step by step answer:
We will first refer to the figures given below for better understanding.
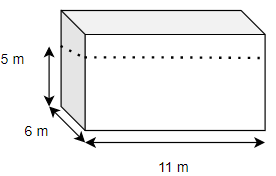
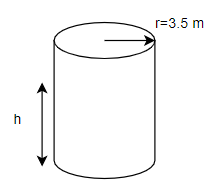
Let us first calculate the volume of water in the rectangular tank.
Length of rectangular tank = 11 m
Breadth of rectangular tank = 6 m
Height of rectangular tank = 5 m
We will substitute these values in the formula for volume of the rectangular tank which is as follows.
Volume of rectangular tank
Now, let us calculate the volume of water in the cylindrical tank.
Radius of cylindrical tank = r = 3.5 m
Height of cylindrical tank = h
Now, we will use the formula for the volume of a cylindrical tank.
Volume of cylindrical tank
Substituting the values in the formula for volume of cylindrical tank, we get
As we know that the volume of water remains the same we can equate the equations (1) and (2).
On equating we get,
We get the height of the cylindrical tank as 8.57 m.
We have been asked to find the height in cm.
So to convert m to cm we will multiply the value of h in m by 100
Hence, the height of water level in a cylindrical tank is 857 cm.
Note: We need to keep in mind that as the same water from the rectangular tank is transferred to the cylindrical tank the volume of water remains same and hence we can equate the equations to find the height of water level in cylindrical tank. Also, keep in mind that all dimensions are given in m but we are asked to find the height of the water level in cm. To avoid too many calculations, it is best to first calculate the height in m and then convert into cm.
Complete step by step answer:
We will first refer to the figures given below for better understanding.


Let us first calculate the volume of water in the rectangular tank.
Length of rectangular tank = 11 m
Breadth of rectangular tank = 6 m
Height of rectangular tank = 5 m
We will substitute these values in the formula for volume of the rectangular tank which is as follows.
Volume of rectangular tank
Now, let us calculate the volume of water in the cylindrical tank.
Radius of cylindrical tank = r = 3.5 m
Height of cylindrical tank = h
Now, we will use the formula for the volume of a cylindrical tank.
Volume of cylindrical tank
Substituting the values in the formula for volume of cylindrical tank, we get
As we know that the volume of water remains the same we can equate the equations (1) and (2).
On equating we get,
We get the height of the cylindrical tank as 8.57 m.
We have been asked to find the height in cm.
So to convert m to cm we will multiply the value of h in m by 100
Hence, the height of water level in a cylindrical tank is 857 cm.
Note: We need to keep in mind that as the same water from the rectangular tank is transferred to the cylindrical tank the volume of water remains same and hence we can equate the equations to find the height of water level in cylindrical tank. Also, keep in mind that all dimensions are given in m but we are asked to find the height of the water level in cm. To avoid too many calculations, it is best to first calculate the height in m and then convert into cm.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




