Question

A regular pentagon is joined to an equilateral triangle whose length of sides is equal to the length of the sides of the regular pentagon. The figure thus obtained is
[a] An irregular hexagon
[b] A regular hexagon
[c] A regular octagon
[d] A regular nonagon.

Answer 1

Hint: Recall the definition of a regular polygon and recall the definitions of a regular pentagon, a regular hexagon, an irregular hexagon, a regular octagon and a regular nonagon and an equilateral triangle. Form the diagram of a regular pentagon on whose side is mounted an equilateral triangle. Find the measure of all the angles of the so formed polygon. Verify which of the options does the polygon belong and hence find the answer.

Complete step-by-step answer:
Before solving the question, we need to understand the definitions of an equilateral triangle, a regular polygon, a pentagon, a hexagon, an octagon, and a nonagon.
Equilateral Triangle- A triangle in which all the sides are equal, and all the angles are equal is called an equilateral triangle.
Regular polygon- A polygon in which all the sides are equal, and all the angles are equal is called a regular polygon.
Regular Pentagon- A regular polygon of 5 sides is called a regular pentagon
Regular Hexagon- A regular polygon of 6 sides is called a regular hexagon
Regular octagon- A regular polygon of 8 sides is called a regular octagon.
Regular Nonagon- A regular polygon of 9 sides is called a regular nonagon.
Irregular hexagon- A polygon of 6 sides which is not regular is called an irregular hexagon.

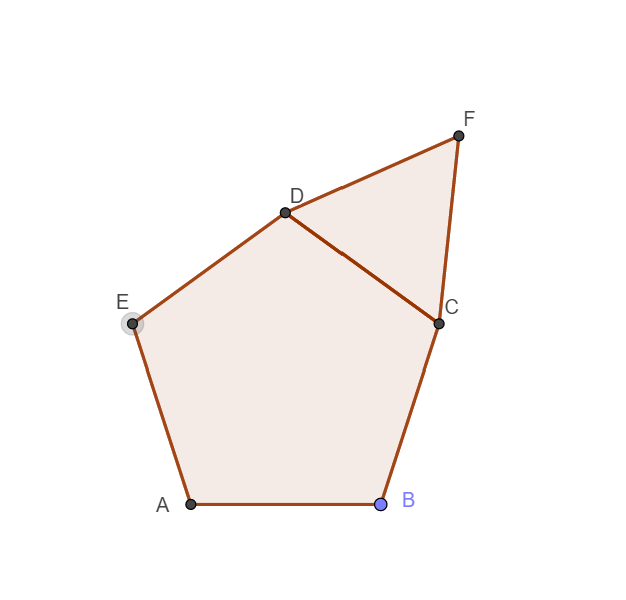
ABCDE is a regular pentagon and on the side DC an equilateral triangle DCF of same side length is mounted.
Now, we know that the measure of an angle of a regular polygon of n sides is $\dfrac{\left( n-2 \right)\times 180}{n}$
Hence, we have
The angle DCB is part of the regular pentagon as we can see from the figure, so the measure of angle DCB is $\dfrac{\left( 5-2 \right)}{5}\times 180=108{}^\circ $
Also, we have an equilateral triangle and hence can write the measure of angle FCD as $\dfrac{3-2}{3}\times 180{}^\circ =60{}^\circ $
Now, we have
$\angle FCB=\angle FCD+\angle DCB=108+60=168{}^\circ $
Also, we have
$\angle ABC=\angle DCB=108{}^\circ $(Because the angles of a regular pentagon are equal).
Hence, the polygon ABCFDE cannot be a regular polygon since the angles are not equal.
Also, the polygon ABCFDE has six sides viz AB, BC, CF, FD, DE and EA.
Hence ABCFDE is a hexagon.
Hence ABCFDE is an irregular hexagon.
Hence option [a] is correct.

Note: A common mistake by most students is that they check if a polygon has all sides equal and if it does then claim that the polygon is a regular polygon. This is incorrect since in only triangles this holds and not in any other polygon. For a polygon to be regular, it must have all sides and all angles equal.