Answer
Verified366k+ views
Hint: Here in this question, we have to explain when a Rhombus is a regular polygon. In order to explain this, first we need to consider a Rhombus and its properties. After that we need to consider the properties of regular polygons. If the conditions or properties are satisfied by the Rhombus, then it’s called a regular polygon, otherwise it’s not a regular polygon.
Complete answer:
A polygon is a regular polygon when all of its sides and all of its interior angles are equal. It means regular polygons must be equilateral (all of its sides are equal) and equiangular (all of its angles are equal).
In geometry, a Rhombus is a four-sided polygon having all the sides equal in length. Also, it is a special type of parallelogram in which opposite sides are parallel, and the opposite angles are equal.
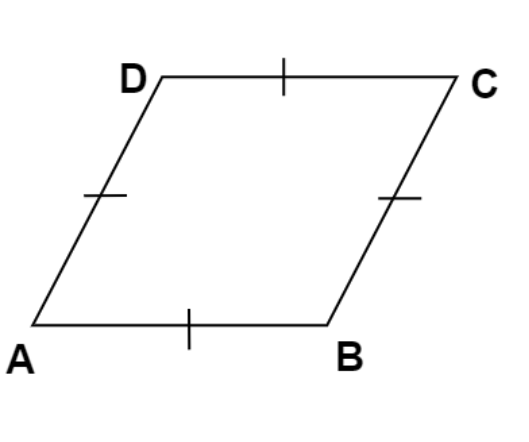
Here, \[AB = BC = CD = DA\]
\[\angle ABC = \angle ADC\] and \[\angle DAB = \angle DCB\]
Now, by the properties of Rhombus,
All the sides are equal and opposite angles are equal, but for a regular polygon all the sides must be equal, and all the interior angles must be equal.
Hence, Rhombus can never be a regular polygon.
Note:
Always remember, a regular polygon should be both equilateral and equiangular. Rhombus is only equilateral but not equiangular. Also, if the rhombus satisfies equiangular condition, then each of its four interior angles must be equal. And we know that the sum of all four interior angles is \[360^\circ \]. Hence, each angle must be a quarter of \[360^\circ \] , that is \[90^\circ \]. Hence, if the rhombus satisfies both the conditions to be a regular polygon then the shape will be a square.
Complete answer:
A polygon is a regular polygon when all of its sides and all of its interior angles are equal. It means regular polygons must be equilateral (all of its sides are equal) and equiangular (all of its angles are equal).
In geometry, a Rhombus is a four-sided polygon having all the sides equal in length. Also, it is a special type of parallelogram in which opposite sides are parallel, and the opposite angles are equal.
Here, \[AB = BC = CD = DA\]
\[\angle ABC = \angle ADC\] and \[\angle DAB = \angle DCB\]
Now, by the properties of Rhombus,
All the sides are equal and opposite angles are equal, but for a regular polygon all the sides must be equal, and all the interior angles must be equal.
Hence, Rhombus can never be a regular polygon.
Note:
Always remember, a regular polygon should be both equilateral and equiangular. Rhombus is only equilateral but not equiangular. Also, if the rhombus satisfies equiangular condition, then each of its four interior angles must be equal. And we know that the sum of all four interior angles is \[360^\circ \]. Hence, each angle must be a quarter of \[360^\circ \] , that is \[90^\circ \]. Hence, if the rhombus satisfies both the conditions to be a regular polygon then the shape will be a square.