Question

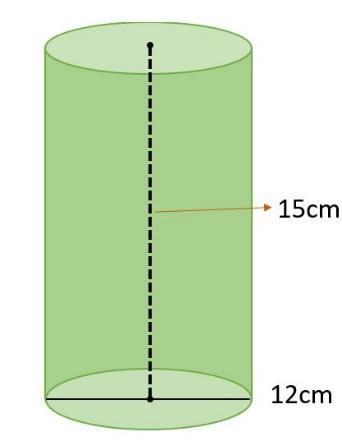
A right circular cylinder having a diameter 12cm and height 15cm is full of ice-cream. The ice-cream is to be filled in cones of height 12cm and diameter 6cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.

Answer 1

Hint: Here, first we have to find the volume of the cylinder using the formula $\pi {{r}^{2}}h$. Next, we have to the find the volume of the ice-cream cone having a hemispherical shape, for that we have to find the volume of the cone by the formula $\dfrac{1}{3}\pi {{r}^{2}}h$ and then find the volume of hemisphere using the formula $\dfrac{2}{3}\pi {{r}^{3}}$. Here, the radius of the cone will be equal to the radius of the hemisphere. At last, find the number of cones which is the volume of the cylinder divided by the sum of the volumes of cone and hemisphere.

Complete step-by-step answer:
We are given a right circular cylinder full of ice-cream. The height and diameter of the cylinder are,
$\begin{align}
  & {{h}_{1}}=15cm \\
 & {{d}_{1}}=12cm \\
\end{align}$
Therefore, radius ${{r}_{1}}$ of the cylinder is,

$\begin{align}
  & {{r}_{1}}=\dfrac{d}{2} \\
 & {{r}_{1}}=\dfrac{12}{2} \\
 & {{r}_{1}}=6cm \\
\end{align}$
Next, we have to find the volume of the cylinder, ${{V}_{1}}$. It is given by,
$\begin{align}
  & {{V}_{1}}=\pi {{r}_{1}}^{2}{{h}_{1}} \\
 & {{V}_{1}}=\pi \times 6\times 6\times 15 \\
 & {{V}_{1}}=540\pi \\
\end{align}$
Hence, the volume of the cylinder is given by ${{V}_{1}}=540\pi c{{m}^{3}}$.
Next, we have to fill the ice-cream in a cone having a hemispherical shape on the top.

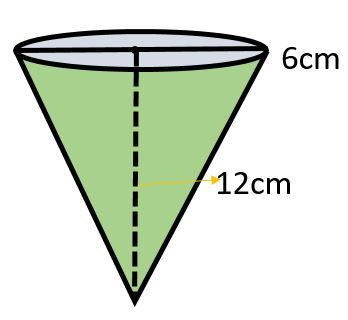
The height and diameter of the cone is given as,
$\begin{align}
  & {{h}_{2}}=12cm \\
 & {{d}_{2}}=6cm \\
\end{align}$
Therefore, the radius ${{r}_{2}}$ of the cone is,
$\begin{align}
  & {{r}_{2}}=\dfrac{{{d}_{2}}}{2} \\
 & {{r}_{2}}=\dfrac{6}{2} \\
 & {{r}_{2}}=3cm \\
\end{align}$
Next, we have to find the volume of the cone. The volume of the cone ${{V}_{2}}$ is given by,
$\begin{align}
  & {{V}_{2}}=\dfrac{1}{3}\pi {{r}_{2}}^{2}{{h}_{2}} \\
 & {{V}_{2}}=\dfrac{1}{3}\pi \times 3\times 3\times 12 \\
 & {{V}_{2}}=36\pi \\
\end{align}$
Hence, the volume of the cone is given by, ${{V}_{2}}=36\pi c{{m}^{3}}$
Since the cone has a hemispherical top, the diameter of the cone is the same as the diameter of the hemisphere.
Therefore, the diameter of the hemisphere is given by
$\begin{align}
  & {{d}_{3}}=6cm \\
 & {{r}_{3}}=\dfrac{{{d}_{3}}}{2} \\
 & {{r}_{3}}=\dfrac{6}{2} \\
 & {{r}_{3}}=3cm \\
\end{align}$
That is, the radius of the hemisphere ${{r}_{3}}=3cm$.
Next, we have to find the volume of the hemisphere. The volume of the hemisphere ${{V}_{3}}$, is given by,
$\begin{align}
  & {{V}_{3}}=\dfrac{2}{3}\pi {{r}_{3}}^{3} \\
 & {{V}_{3}}=\dfrac{2}{3}\pi \times 3\times 3\times 3 \\
 & {{V}_{3}}=18\pi \\
\end{align}$
Hence, the volume of the hemisphere is given by, ${{V}_{3}}=18\pi c{{m}^{3}}$.
Now, we have to find the number of cones which can be filled with ice-cream.
Number of ice-cream cones, n is obtained by:
 $\begin{align}
  & n=\dfrac{Volume\text{ }of\text{ }the\text{ }cylinder}{Volume\text{ }of\text{ }the\text{ }cone+Volume\text{ }of\text{ }the\text{ }hemisphere} \\
 & n=\dfrac{{{V}_{1}}}{{{V}_{2}}+{{V}_{3}}} \\
 & n=\dfrac{540\pi }{36\pi +18\pi } \\
 & n=\dfrac{540\pi }{54\pi } \\
\end{align}$
By cancellation, we get, $n=10$
Therefore, the number of cones that can be filled with ice-cream is 10.

Note: Here, we have to calculate the number of ice-cream filled cones, so while considering cones you have to take, volume of cone + volume of hemisphere, don’t take the volume of cone alone which may lead to a wrong answer.