Question

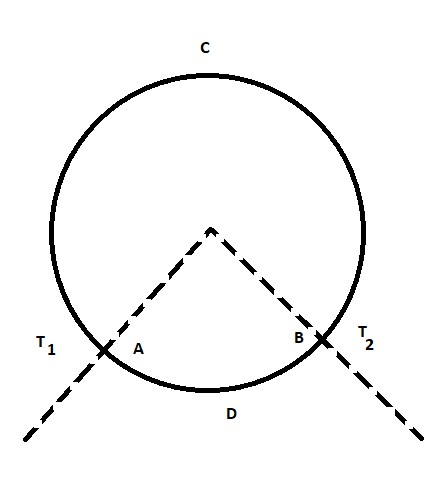
A ring consisting of two parts \[ADB\] and \[ACB\] of same conductivity \[k\] carries an amount of heat \[H\] . The \[ADB\] part is now replaced with another metal keeping the temperatures \[{T_1}\] and \[{T_2}\] constant. The heat carried increases to \[2H\] . What should be the conductivity of the new \[ADB\] part? Given \[\dfrac{{ACB}}{{ADB}} = 3\]

A. \[\dfrac{7}{3}k\]
B. \[2k\]
C. \[\dfrac{5}{2}k\]
D. \[3k\]

Answer 1

Hint: First of all, we will find the respective lengths of the two parts. After that we will find the net resistance before and after replacement of the metal part. The new resistance of the part will be half the previous value. We will manipulate accordingly to obtain the result.

Complete step by step answer:
In the given problem, we are supplied the following data:
The ring has two parts \[ADB\] and \[ACB\] .
Both the parts have the same conductivity in the first case.
Due to the flow of current through the ring, the heat energy is generated in the ring whose value is \[H\] .
After the \[ADB\] part is replaced with another metal.
Due to this the conductivity will be different, as the different metals have different conductivity.
The temperatures are kept constant for both the cases.
The magnitude of heat generated in the second case is twice that of the first.
We are asked to find the conductivity of the new metal which was just added.
To solve this problem, we will begin with:
Since, we are given,
\[\dfrac{{ACB}}{{ADB}} = 3\]
Then we can say that:
The length of the part \[ADB\] is \[l\] .
The length of the part \[ACB\] is \[3l\] .

Now we find the net resistance of the ring, which is given by the following expression:
Since, both the parts can be assumed to have been connected in parallel.
Let the net resistance of the ring be \[R\] .
So,
\[\dfrac{1}{R} = \dfrac{1}{{{R_{{\text{ACB}}}}}} + \dfrac{1}{{{R_{{\text{ABD}}}}}}\] …… (1)
Where,
\[{R_{{\text{ACB}}}}\] indicates the resistance of the part \[ACB\] .
\[{R_{{\text{ABD}}}}\] indicates the resistance of the part \[ADB\] .

Again, the resistance of the part \[ACB\] is given by the formula:
\[{R_{{\text{ACB}}}} = \dfrac{L}{{kA}}\]
Where,
\[L\] indicates length of the conductor.
\[k\] indicates conductivity.
\[A\] indicates a cross-sectional area.
We can write the above expression as:
\[{R_{{\text{ACB}}}} = \dfrac{{3l}}{{kA}}\]
The resistance of the part \[ADB\] is given by the formula:
\[{R_{{\text{ADB}}}} = \dfrac{L}{{kA}}\]
We can write the above expression as:
\[{R_{{\text{ADB}}}} = \dfrac{l}{{kA}}\]

Now, substituting the required values in the equation (1), we get:
\[\dfrac{1}{R} = \dfrac{1}{{\left( {\dfrac{{3l}}{{kA}}} \right)}} + \dfrac{1}{{\left( {\dfrac{l}{{kA}}} \right)}}\]
\[\dfrac{1}{R} = \dfrac{{kA}}{{3l}} + \dfrac{{kA}}{l}\]
\[\dfrac{1}{R} = \dfrac{{4kA}}{{3l}}\] …… (2)

When we replace the \[ADB\] part, and add other material whose conductivity is taken as \[k'\] , the heat generated becomes \[2H\] . But the potential difference is constant, as the temperatures are kept constant. So, it is obvious that the current becomes double in that case. And the new resistance \[R'\] , becomes half the previous resistance.
So, we can write:
\[R' = \dfrac{R}{2}\]
Again, the net resistance of the ring after replacing the part becomes:
\[\dfrac{1}{{R'}} = \dfrac{{kA}}{{3l}} + \dfrac{{k'A}}{l}\] …… (3)
Now, using equation (2) in equation (3), we get:
\[
\dfrac{2}{R} = \dfrac{{kA}}{{3l}} + \dfrac{{k'A}}{l} \\
  2 \times \dfrac{{4kA}}{{3l}} = \dfrac{A}{l}\left( {\dfrac{k}{3} + k'} \right) \\
\dfrac{8}{3}k = \dfrac{{k + 3k'}}{3} \\
  k' = \dfrac{7}{3}k \\
\]
Hence, the conductivity of the new \[ADB\] part \[\dfrac{7}{3}k\] .
The correct option is A.

Note:While solving this problem, remember that voltage is constant as we are said that the temperature remains constant. Again, since the voltage is constant but the heat generated becomes twice, then the resistance must become half in order to ease the current flow.