Question

A ring has mass $M$ ,radius $R$. A point mass $m$ is placed at a distance $x$ on the axial line as shown in the figure. Find $x$ so that force experienced is maximum.

A. $\dfrac{R}{{3\varepsilon }}$
B.$\dfrac{R}{2}$
C. $\dfrac{R}{{\sqrt 2 }}$
D. $\dfrac{R}{{\sqrt 3 }}$

Answer 1

Hint: One of the masses is a ring. Consider a small element $dm$ which makes an angle $\theta $ with the center of the ring.
$dm = \dfrac{M}{{2\pi }}d\theta $

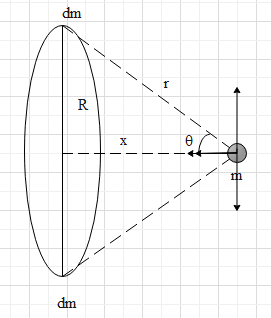
Because of symmetry if we consider two diametrically opposite points. Then the vertical component of forces of both these points on the point mass $m$ will cancel out and the horizontal component gets added up.
The horizontal component is $\cos \theta $.
Since, $\cos \theta $ is equal to adjacent side by hypotenuse,
Here using Pythagoras theorem
Hypotenuse, $r = \sqrt {{R^2} + {x^2}} $
$\cos \theta = \dfrac{x}{{\sqrt {{R^2} + {x^2}} }}$
Therefore,
$dF = \dfrac{{G\dfrac{M}{{2\pi }}d\theta m}}{{{r^2}}} \times 2 \times \dfrac{x}{{\sqrt {{R^2} + {x^2}} }}$
On integrating we can find $F$.
When, $F$ is maximum
$\dfrac{{dF}}{{dx}} = 0$

Complete step by step answer:
According to the law of gravitation force of gravity is directly proportional to the product of the mass of the bodies and inversely proportional to the square of the distance between them.
In equation form it is given as
$F = \dfrac{{GMm}}{{{r^2}}}$
This is for the case of a point mass.
Here one of the masses is a ring. Let us consider a small element $dm$ which makes an angle $\theta $ with the center of the Ring.

$dm = \dfrac{M}{{2\pi }}d\theta $
Because of symmetry if we consider two diametrically opposite points. Then the vertical component of forces of both these points on the point mass $m$ will cancel out and the horizontal component gets added up.
The horizontal component is $\cos \theta $.
Since, $\cos \theta $ is equal to adjacent side by hypotenuse,
$\cos \theta = \dfrac{x}{{\sqrt {{R^2} + {x^2}} }}$
Here using Pythagoras theorem
Hypotenuse, $r = \sqrt {{R^2} + {x^2}} $
Therefore,
$dF = \dfrac{{G\dfrac{M}{{2\pi }}d\theta m}}{{{r^2}}} \times 2 \times \dfrac{x}{{\sqrt {{R^2} + {x^2}} }}$
Thus,
$F = \int\limits_0^{2\pi } {\dfrac{{G\dfrac{M}{{2\pi }}d\theta m}}{{{r^2}}}} = \dfrac{{GM2\pi m}}{{2\pi ({R^2} + {X^2})}}\dfrac{{2x}}{{\sqrt {{R^2} + {x^2}} }}$
$F = \dfrac{{GMmx}}{{{{\left( {{R^2} + {x^2}} \right)}^{\dfrac{3}{2}}}}}$
When, $F$ is maximum
$
  \dfrac{{dF}}{{dx}} = 0 \\
   \Rightarrow x \times \dfrac{{ - 3}}{2}{\left( {{R^2} + {x^2}} \right)^{\dfrac{{ - 5}}{2}}} \times 2x + {\left( {{R^2} + {x^2}} \right)^{\dfrac{{ - 3}}{2}}} = 0 \\
   \Rightarrow 2{x^2} = {R^2} \\
   \Rightarrow x = \dfrac{R}{{\sqrt 2 }} \\
 $
So, the correct option is option C.

Note:
- Remember that the equation $F = \dfrac{{GMm}}{{{r^2}}}$ is used when both the masses are point masses.
- In this case, one of the masses is a distributed mass. So, we need to modify the equation according to the situation.
- Also, remember that due to the symmetry of the ring if we consider two diametrically opposite points. Then the vertical component of forces of both these points on the point mass $m$ will cancel out and the horizontal component gets added up.