Question

A road which is 7 m wide surrounds a circular park whose circumference is 352 m. Find the area of the road.

Answer 1

Hint:
Let us find the radius of the park using the circumference given and add the width of the road to it and consider it as the new radius, and find the area of the circle with radius newly found, but we have to find the area of the road. To find the area of the road we will subtract the area of the park from the area found using the new radius.

Formula used:
The area of a circle with radius r is \[\pi {r^2}\]
The circumference of a circle with radius r is \[2\pi r\]

Complete step-by-step answer:
It is given that,
A road which is 7 m wide surrounds a circular park whose circumference is 352 m.
 

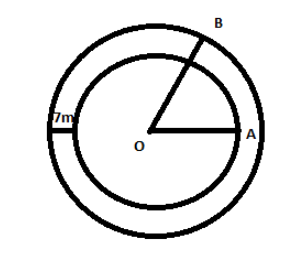
In the given figure let us consider OA as the radius of the park, and OB is the total radius
The circumference of the circular park is 352 m.
The circumference of a circle with radius r is\[2\pi r\].
So, let us equate both the formula and value we get,
\[2\pi r = 352\]
Let us divide both sides of the above equation by \[2\pi \]we get,
\[r = \dfrac{{352}}{{2\pi }}\]
Let us now substitute the value of \[\pi \]as we know that\[\pi = \dfrac{{22}}{7}\], we get
\[r = \dfrac{{352}}{{2 \times \dfrac{{22}}{7}}}\]
By solving the above equation we get the radius of the park.
\[r = 56m\]
Therefore the radius of the circular park is 56m.
Now let us find the area of the park which will be useful in calculating the area of the road.
The area of the circular park is\[\pi {r^2}\]on substituting the value of r, we get,
The area of the circular park is\[\dfrac{{22}}{7} \times 56 \times 56{m^2}\]
The road is 7 m wide and surrounds the circular park.
We have to find out the area of the road which we can get by subtracting the area of the circular park from the area of the circular portion including the road and the circular park.
That is,
The area of the road = The area of the circular area of radius (56+7) m – the area of the circular park
= The area of the circular area of radius 63 m – the area of the circular park
Now let us find the area of circular area of radius 63m,
The area of the circular area of radius is\[\pi {r^2}\]
Let us substitute the value of r, we get
The area is\[\dfrac{{22}}{7} \times 63 \times 63{m^2}\]
Therefore, the area of the road is found by solving the equations below,
The area of the road\[ = \dfrac{{22}}{7} \times 63 \times 63 - \dfrac{{22}}{7} \times 56 \times 56\]
By solving the above equation and taking the common terms out of it we get,
\[ = 22(9 \times 63 - 8 \times 56)\]
Let us multiply the equation and proceed further therefore we get,
The area of the road \[ = 22(567 - 448)\]\[ = 22 \times 119 = 2618{m^2}\]
Hence, the area of the road is \[2618{m^2}\]

Note:
The value of π is used here, π=\[\dfrac{{22}}{7}\] .
We can find the area of a ring surrounds a circular area by subtracting the area of the smaller circle from the larger circle.
Using the inner radius and outer radius we can also find the area of the road using the formula
Area of ring $ = \pi ({R^2} - {r^2})$
Where R is the outer radius and r is the inner radius,
Here R=63 m and r= 56 m
Therefore the area of the road $ = \pi ({63^2} - {56^2})$
By substituting the value π=\[\dfrac{{22}}{7}\] we get,
The area of the road\[ = \dfrac{{22}}{7} \times (63 \times 63 - \times 56 \times 56)\]\[ = 2618{m^2}\]