Question

A rocket with a lift-off mass 20,000kg is blasted upwards with an initial acceleration of\[5.0m{{s}^{-2}}\]. Calculate the initial thrust (force) of the blast.

Answer 1

Hint: A rocket will require an upward thrust to take off and that is the initial thrust it will have. Thrust is a force which is generated due to acceleration of fuel or gas, therefore a rocket will have a thrust while launching. Thrust is given by the same formula as the force. By using Newton's second law we can calculate the force.

Formula used:
\[F=ma\]

Complete answer:
While launching the rocket, it has initial acceleration of \[5.0m{{s}^{-2}}\] and the rocket will require an upward thrust to take off and so it has to work against the acceleration due to gravity. A diagrammatic representation can be given as

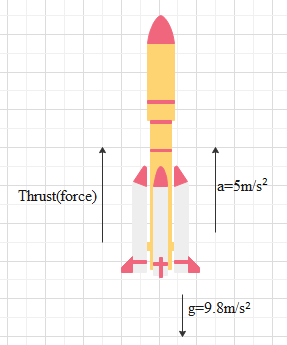
To overcome the acceleration due to gravity, the rocket will actually have acceleration which will be sum of acceleration due to gravity and initial acceleration of the rocket and it is given as
\[a'=a+g\]
Where a is initial acceleration given and g is the acceleration due to gravity and a’ is the acceleration which rocket will have.
Substituting \[a=5m/{{s}^{2}}\text{ and }g=9.8m/{{s}^{2}}\]in above equation, we get
\[\begin{align}
  & a'=5+9.8 \\
 & a'=14.8 \\
\end{align}\]
Now according to the second law of motion, force is the product of mass into acceleration. Therefore, upward thrust is given as
\[F=ma'\]
Substituting\[m=20,000kg=2\times {{10}^{4}}kg\text{ and }a'=14.8\], we get
\[\begin{align}
  & F=\left( 2\times {{10}^{4}} \right)\left( 14.8 \right) \\
 & F=29.6\times {{10}^{4}}N \\
 & F=2.96\times {{10}^{5}}N \\
\end{align}\]
Hence \[2.96\times {{10}^{5}}N\] upward thrust will be required for the blast.

Note:
As thrust is given by the same formula of force and we have given the mass and initial acceleration, one can directly calculate the force without considering acceleration due to gravity which will give the wrong result. Another mistake which can be made is subtracting the acceleration due to gravity by the initial acceleration of the rocket.