Question

A rod $AB$ is shown in figure. End A of the rod is fixed on the ground. Block is moving with velocity. \[\sqrt 3 m/s\] towards the right. The velocity of end B of rod when rod makes an angle of \[60^\circ \] with the ground is:

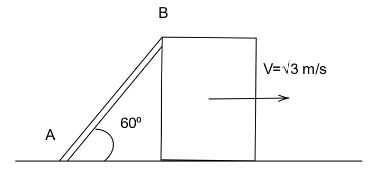
A. \[\sqrt 3 \,m/s\]
B. \[2\,m/s\]
C. \[2\sqrt 3 \,m/s\]
D. \[3\,m/s\]

Answer 1

Hint: We are asked to find the velocity at the end B of the rod when the velocity of the block and angle is given. For this, we can divide or resolve the velocity at point B into two components. Then, once we have done this process, we can move onto finding the asked velocity in the question, we can divide the given velocity by the value of velocity given by the x-component.

Formulas used:
A vector can be split into two components, the $x$ component and the $y$ component.
The x component being \[{V_x} = V\cos \theta \].
The y component being \[{V_y} = V\sin \theta \].

Complete step by step answer:

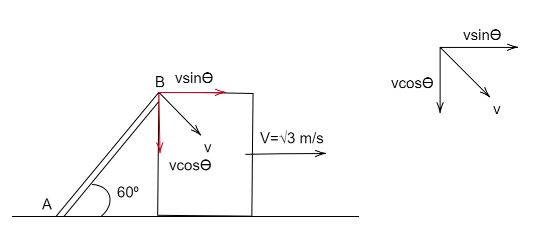
We can start by writing down the values given in the question, the velocity of the block is, \[\sqrt 3 m/s\]. The angle the point A makes with the ground is, \[60^\circ \]. From the data given above, we can find the angle the point B makes with the edge of the block. This angle can be found by \[180 - \left( {60 + 90} \right) = 30\].

The $x$ component of the velocity caused at this angle will be,
\[{V_x} = V\cos 30 = V\dfrac{{\sqrt 3 }}{2}\]
And the y component of the velocity caused will be,
\[{V_y} = V\sin 30 = V\dfrac{1}{2}\]
The movement of the block is in the x direction; hence we equate the x component to the velocity of the block and get
\[V\cos 30 = \sqrt 3 \\
\Rightarrow V = \dfrac{{\sqrt 3 }}{{\cos 30}} \\
\Rightarrow V = \dfrac{{\sqrt 3 \times 2}}{{\sqrt 3 }} \\
\therefore V = 2\,m/s\]

Therefore, the right answer is option B.

Note: A vector, in simple terms, is a quantity that has both magnitude and direction. A vector can be split into its constituent components. Here we deal with a vector in two-dimensional space, that is a plane. Hence we only split into its two components, namely the x and y components. Vectors help us represent the position, displacement, velocity acceleration, etc. Vector calculation is a very essential part of problem-solving.