
A rod is free to rotate about the Y axis as shown. It begins to rotate from its unstable equilibrium position. When it has turned through an angle $\theta $, its angular velocity $\omega $is given as

A. $\sqrt{\dfrac{6g}{l}}\sin \theta $
B. $\sqrt{\dfrac{6g}{l}}\sin \left( \dfrac{\theta }{2} \right)$
C. $\sqrt{\dfrac{6g}{l}}\cos \dfrac{\theta }{2}$
D. $\sqrt{\dfrac{6g}{l}}\cos \theta $

Answer
500.4k+ views
Hint: As a very first step, one could read the question and find that the system’s total mechanical energy is conserved. Now you could find that the change of centre of gravity takes place and hence you could find the related change in potential energy and then equate it to the kinetic energy and hence find the answer.
Complete step by step solution:
In the question, we are given a uniform rod of length l that is free to rotate in a vertical plane about a certain fixed axis through B. The rotation of the rod begins from its unstable equilibrium position. We are supposed to find the angular velocity $\omega $when the rod is turned through an angle $\theta $.
Since only the weight of the body, which is a conservative force acts on the rod, the total mechanical energy will be conserved.
Mechanical energy will be the sum of kinetic and potential energy.
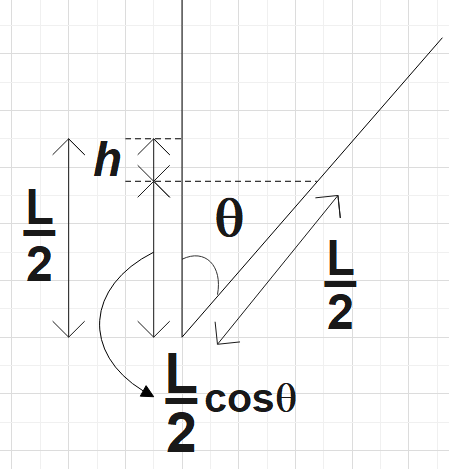
So, the above figure gives the height h through which the centre of gravity has shifted. From the figure we find this length to be,
$h=\dfrac{L}{2}-\dfrac{L}{2}\cos \theta =\dfrac{L}{2}\left( 1-\cos \theta \right)$…………………………………….. (1)
The change in potential energy would be,
$\Delta PE=mgh=mg\dfrac{L}{2}\left( 1-\cos \theta \right)$…………………………………….. (2)
Rotational kinetic energy would be given by,
$KE=\dfrac{1}{2}I{{\omega }^{2}}$
Where, moment of inertia of a rod would be,
$I=\dfrac{m{{L}^{2}}}{3}$
\[\Rightarrow KE=\dfrac{m{{L}^{2}}{{\omega }^{2}}}{6}\]………………………………………………. (3)
We could equate (2) and (3) as the system is conservative,
$mg\dfrac{L}{2}\left( 1-\cos \theta \right)=\dfrac{m{{L}^{2}}{{\omega }^{2}}}{6}$
$\Rightarrow {{\omega }^{2}}=\dfrac{3g\left( 1-\cos \theta \right)}{L}=\dfrac{6g{{\sin }^{2}}\dfrac{\theta }{2}}{L}$
$\therefore \omega =\sqrt{\dfrac{6g}{L}}\sin \dfrac{\theta }{2}$
Therefore, we found the angular velocity to be, $\omega =\sqrt{\dfrac{6g}{L}}\sin \dfrac{\theta }{2}$
Hence, option B is correct.
Note: Now, you may be wondering why haven’t we discussed anything about the translational kinetic energy. This is simply because it just doesn’t exist here. You may find that the point at which the rod is hinged doesn’t move and is fixed and thereby we shouldn’t worry about the translational motion and also the related kinetic energy.
Complete step by step solution:
In the question, we are given a uniform rod of length l that is free to rotate in a vertical plane about a certain fixed axis through B. The rotation of the rod begins from its unstable equilibrium position. We are supposed to find the angular velocity $\omega $when the rod is turned through an angle $\theta $.
Since only the weight of the body, which is a conservative force acts on the rod, the total mechanical energy will be conserved.
Mechanical energy will be the sum of kinetic and potential energy.
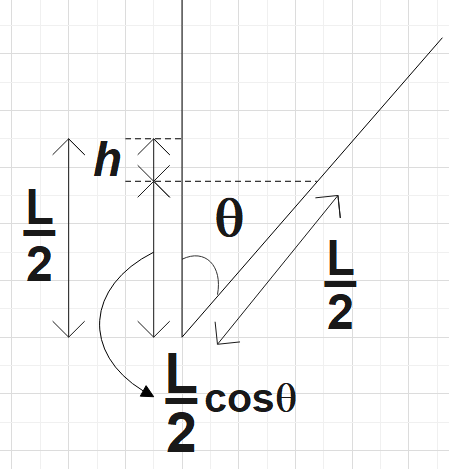
So, the above figure gives the height h through which the centre of gravity has shifted. From the figure we find this length to be,
$h=\dfrac{L}{2}-\dfrac{L}{2}\cos \theta =\dfrac{L}{2}\left( 1-\cos \theta \right)$…………………………………….. (1)
The change in potential energy would be,
$\Delta PE=mgh=mg\dfrac{L}{2}\left( 1-\cos \theta \right)$…………………………………….. (2)
Rotational kinetic energy would be given by,
$KE=\dfrac{1}{2}I{{\omega }^{2}}$
Where, moment of inertia of a rod would be,
$I=\dfrac{m{{L}^{2}}}{3}$
\[\Rightarrow KE=\dfrac{m{{L}^{2}}{{\omega }^{2}}}{6}\]………………………………………………. (3)
We could equate (2) and (3) as the system is conservative,
$mg\dfrac{L}{2}\left( 1-\cos \theta \right)=\dfrac{m{{L}^{2}}{{\omega }^{2}}}{6}$
$\Rightarrow {{\omega }^{2}}=\dfrac{3g\left( 1-\cos \theta \right)}{L}=\dfrac{6g{{\sin }^{2}}\dfrac{\theta }{2}}{L}$
$\therefore \omega =\sqrt{\dfrac{6g}{L}}\sin \dfrac{\theta }{2}$
Therefore, we found the angular velocity to be, $\omega =\sqrt{\dfrac{6g}{L}}\sin \dfrac{\theta }{2}$
Hence, option B is correct.
Note: Now, you may be wondering why haven’t we discussed anything about the translational kinetic energy. This is simply because it just doesn’t exist here. You may find that the point at which the rod is hinged doesn’t move and is fixed and thereby we shouldn’t worry about the translational motion and also the related kinetic energy.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE




