Question

A rod OA of mass 4kg is held in horizontal position by a massless string AB as shown in figure. Length of the rod is 2m. Find

(a) tension in the string
(b) net force exerted by hinge on the rod. ($g=10m{{s}^{-2}}$)

Answer 1

Hint: The given rod is in an equilibrium condition, which means that the net torque and the net force on the rod is zero. Therefore, equate the net torque about the hinges point equal to equal to find the tension. Then equate the net force to zero to find the hinge force.
Formula used:
${{F}_{g}}=mg$
$\tau =Fr$

Complete answer:
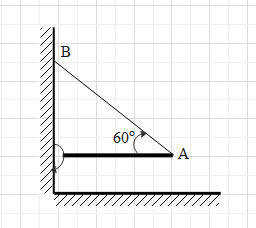
(a) The string will experience a tension in it because the rod will be pulling it downwards due to the gravitational force. Let the tension in the string be T.
We can see that the rod is in equilibrium. This means that the net torque on the rod is zero. Let us analyse the force on the rod.
The earth will exert a gravitational force on the rod in the downward direction. The magnitude of gravitational force on a body is given as ${{F}_{g}}=mg$, where m is the mass of the body and g is acceleration due to gravity. The gravitational force will be at the centre of mass of the body. Therefore, the gravitational force on the rod is acting on the centre of the rod (i.e. centre of mass).
In this case, m = 4kg and $g=10m{{s}^{-2}}$.
${{F}_{g}}=4\times 10=40N$.

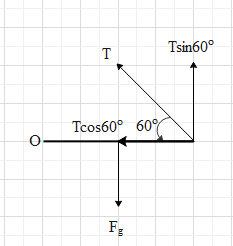
Due to the tension in the string, the rod will experience a force as shown. Resolve the tension into its horizontal and vertical components.
The horizontal component of the tension will be $T\cos {{60}^{\circ }}=T\left( \dfrac{1}{2} \right)=\dfrac{T}{2}$.
And its vertical component will be $T\sin {{60}^{\circ }}=T\left( \dfrac{\sqrt{3}}{2} \right)=\dfrac{\sqrt{3}T}{2}$.
Let us calculate the torque about the hinge point. The magnitude of torque at a point about a its hinged point is given as $\tau =Fr$, where r is the distance between the hinged point and the point of force and F is the force perpendicular to r.
Let us consider the torque in clockwise direction as positive torque and the torque in anticlockwise direction as negative torque.
Therefore, the torque created by the gravitational force is ${{\tau }_{1}}={{F}_{g}}\dfrac{l}{2}=40\times \dfrac{2}{2}=40Nm$.
The torque created by the tension is ${{\tau }_{2}}=-\dfrac{\sqrt{3}T}{2}l=-\dfrac{\sqrt{3}T}{2}(2)=-\sqrt{3}T$.
Hence, the net torque is $\tau ={{\tau }_{1}}-{{\tau }_{2}}=40-\sqrt{3}T$.
But we know that $\tau =0$.
$\Rightarrow 40-\sqrt{3}T=0$
$\Rightarrow T=\dfrac{40}{\sqrt{3}}N$.
(b) The rod is in translational equilibrium too. Hence, the net force on the rod in the horizontal and vertical directions will be zero.

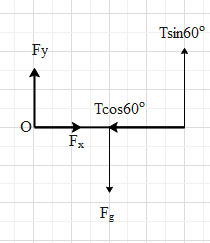
For this, the hinge will apply a force (F) on the rod. Let the horizontal component of the hinge be ${{F}_{x}}$ and its vertical component be ${{F}_{y}}$.
Therefore, the net force in the vertical direction is ${{F}_{y,net}}=-{{F}_{g}}+\dfrac{\sqrt{3}T}{2}+{{F}_{y}}$.
$\Rightarrow {{F}_{y,net}}=-40+\dfrac{\sqrt{3}}{2}\left( \dfrac{40}{\sqrt{3}} \right)+{{F}_{y}}$
But ${{F}_{y,net}}=0$
$\Rightarrow -40+20+{{F}_{y}}=0$
$\Rightarrow {{F}_{y}}=20N$
The net force in the horizontal direction is ${{F}_{x,net}}=-\dfrac{T}{2}+{{F}_{x}}$.
$\Rightarrow {{F}_{x,net}}=-\dfrac{1}{2}\left( \dfrac{40}{\sqrt{3}} \right)+{{F}_{x}}$
But ${{F}_{x,net}}=0$
a
$\Rightarrow {{F}_{x}}=\dfrac{20}{\sqrt{3}}N$
Hence, the force exerted by the hinge is $F=\sqrt{F_{x}^{2}+F_{y}^{2}}=\sqrt{\dfrac{400}{3}+400}=20\sqrt{\dfrac{4}{3}}=\dfrac{40}{\sqrt{3}}N$.

Note:
Remember that we should always check the rotational equilibrium first and then translation equilibrium.In the given case, students may make a mistake by neglecting the rotational equilibrium. If we do that, we will be neglecting the hinge force and the value of the tension in the string will be incorrect.