Question

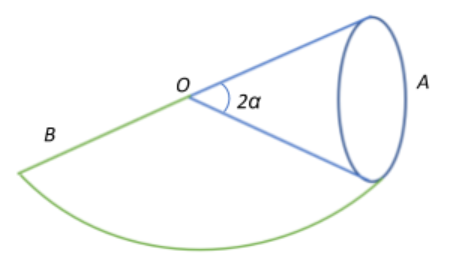
A round cone A of mass $m =3.2\;kg$ and half angle $\alpha=10^{\circ}$ rolls uniformly and without slipping along a round conical surface B so that its apex O remains stationary. The centre of gravity of the cone A is at the same level as the point O and at a distance $l=17\;cm$ from it. Find the static friction acting on the cone A, if radial velocity $\omega = 1.0\;rad.s^{-1}$

Answer 1

Hint: Begin by listing out all the forces that influence the state of rest and motion of the cone. In other words, we have the gravitational force, corresponding normal reaction force, centrifugal force as a result of the fixed apex and moving base of the cone, and the frictional force between the cone A and the surface B. Resolve the forces into their directional components.
At equilibrium determine the expressions for the net force in the horizontal and vertical directions. Rearrange the equations to suitably arrive at an expression for the static frictional force, following which you can substitute the given parameter values to obtain the appropriate result.

Formula used: Gravitational force $F_g = mg$
Centrifugal force $F_c = m\omega^2 l$

Complete step by step answer:
We are given that the mass of the cone $m = 3.2\;kg$.
The conical half-angle $\alpha =10^{\circ}$
The cone moves around the surface B in such a way that the apex O remains fixed at its initial position.
Let us begin by accounting for all influencing forces and resolving them into their corresponding directional components.
The cone possesses mass, and consequently experiences a gravitational force due to the gravitational acceleration acting on the cone by virtue of its placement on the conical surface B. In response to this gravitational force directed downwards, the surface B exerts a reaction force directed normally upwards, passing through the centre of gravity of the cone.
We resolve this normal reaction into its directional components in order to deduce the component of this normal reaction force that balances out the gravitational force since the effective normal reaction is not geometrically aligned with the gravitational force.
Then we have the frictional force that acts along the lateral surface of the cone, between the cone and the surface B as shown in the figure. This frictional force can also be resolved into respective directional components since it acts in a direction inclined with the axis of the cone. Thus, the angle that this force makes with the axis of the cone is geometrically equivalent to the half-angle of the cone.

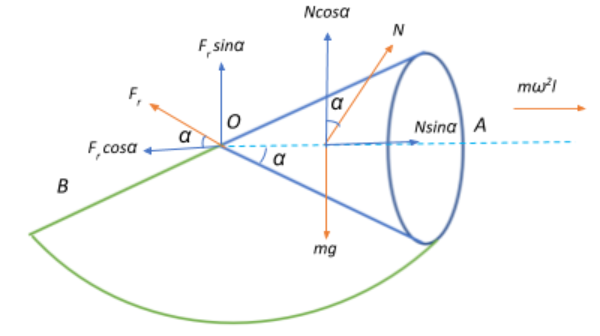
Finally, we have the centrifugal force that the cone is subjected to as a result of having its apex fixed in position while the base moves about this point over the surface B. If the cone possesses a tangential velocity v as it traces an angular path about its centre of gravity at a distance $l$, then the centrifugal force acting on the axis of the cone can be given as:
$F_{c} = \dfrac{mv^2}{l}$.
Since the cone undergoes an angular motion about the conical surface B, the angular velocity with which it traverses the path can be given as $\omega = \dfrac{v}{l} \Rightarrow v = \omega l$
$\Rightarrow F_{c} = \dfrac{m(\omega^2 l^2)}{l} = m\omega^2 l$
From the free body diagram that we’ve thus obtained we can now determine the force equations at equilibrium.
We have along the vertical axis:
$Ncos\alpha -mg+f_r sin\alpha =0$
$\Rightarrow N = \dfrac{1}{cos\alpha}.(-f_r sin\alpha + mg)$
And along the horizontal axis we get:
$f_r cos\alpha -Nsin\alpha-m\omega^2 l = 0$
Substituting for N that we derived earlier:
$f_{r} cos\alpha - \dfrac{sin\alpha}{cos\alpha}.(-f_r sin\alpha + mg) – m\omega^2 l = 0$
Solving for $f_r$:
$f_{r}cos^2\alpha – sin\alpha.(-f_r sin\alpha + mg) – m\omega^2 l cos\alpha = 0$
$\Rightarrow f_r (cos^2\alpha + sin^2 \alpha) - \left(mgsin\alpha + m\omega^2 l cos\alpha\right)=0$
Since $(cos^2\alpha + sin^2 \alpha) =1$, we get:
$\Rightarrow f_r = \left(mgsin\alpha + m\omega^2 l cos\alpha\right)$
$\Rightarrow f_r = mg\left(sin\alpha + \dfrac{\omega^2 l}{g} cos\alpha\right)$
Substituting $m = 3.2\;kg$, $g=9.8\;ms^{-2}$, $\alpha =10^{\circ}$, $l = 17\;cm = 0.17\;m$ and $\omega = 1.0\;rad.s^{-1}$:
$\Rightarrow f_r = (3.2 \times 9.8).\left(sin(10^{\circ}) + \dfrac{1^2 \times 0.17}{9.8}. cos(10^{\circ}) \right)$
$\Rightarrow f_r = (31.36). \left(0.17 + 0.017.(0.98)\right)$
$\Rightarrow f_r = 5.85\;N$

Therefore, the static friction force is found to be $5.85 \approx 6\;N$.

Note: Recall that we take the length of the cone as the radius along which the centrifugal force acts since it is along this axis of the cone with the fixed apex that the cone executes its rolling motion.
Also, remember that it is always helpful to resolve the influencing forces into their components as this will give us a clear picture of which forces contribute in which direction. Failure to do this will result in inconsistent or variably estimated results since we end up accounting for the non-influencing forces or the ones that may in fact, cancel each other out
While resolving the forces into their horizontal and vertical components, remember to assign the $sine$ and $cosine$ values correctly since it is a common misconception that the horizontal side is the $cosine$ part and the vertical side is the $sine$ part.
The correct way to go about this would be to establish that the component that is adjacent to $\alpha$ assumes a $cosine$ value, whereas the component that is opposite to $\alpha$ assumes a $sine$ value.