Question

A satellite is orbiting around the earth. The centripetal force acting on the satellite is F. The force of the satellite on the earth is also F. The net force on the satellite is:
A. F
B. zero
C. 2F
D. $\dfrac{F}{2}$

Answer 1

Hint: A centripetal force is a force that makes a body follow a curved path. The direction is always orthogonal to the motion of the body and towards the fixed point of the instantaneous center of curvature of the path. It is basically the force that keeps the body moving around a fixed point.

Complete step by step answer:
In non-ideal cases, the circular motion of a body will not have constant angular velocity but it will slow down or pick up pace regularly. The total acceleration of a body moving in a circular motion is the resultant of two types of accelerations, namely Centripetal and Tangential acceleration.
$\overrightarrow a = {\overrightarrow a _c} + {\overrightarrow a _t}$
Let us consider a non-uniform circular motion as shown:

In a non-uniform circular motion, the body not only changes its angular velocity per unit time but also, the direction of the velocity vector. Since the velocity vector, which is a tangent to the direction of motion of the body, keeps changing every second, we get an additional component of acceleration. This component of acceleration is called Tangential acceleration.
Tangential acceleration, $\left| {{a_t}} \right| = r\alpha $
$\alpha $is called the angular acceleration, which means the change in angular velocity in radians per second.
$\alpha = \dfrac{\omega }{t}$
There is one more component of acceleration, for the actual change in the velocity per unit time and is directed towards the center of the circle. This is called Centripetal acceleration. This is also called Radial acceleration.
Centripetal acceleration, $\left| {{a_c}} \right| = \dfrac{{{v^2}}}{r}$
The force associated with its centripetal acceleration is called centripetal force. It is equal to the mass times the centripetal acceleration.
$F = m{a_c} $
$\Rightarrow F= \dfrac{{m{v^2}}}{r}$
When the satellite is rotating about the axis of the Earth, it is the same centripetal force that keeps the satellite moving in circles.

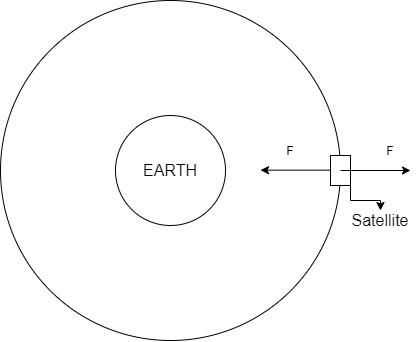
The gravitational force acts on the satellite by the Earth.
Gravitational force by satellite on Earth, $F = \dfrac{{GMm}}{{{r^2}}}$
where $G$ is the gravitational constant, $M$ is the mass of earth, $m$ is the mass of the satellite and $r$ is the radius of the satellite orbit.
As a reaction to this force, there is an equal and opposite reaction force acted by the satellite on the Earth. This force becomes the reactional centrifugal force that pushes the satellite away from the Earth.
Thus, the centripetal force is balanced by the centrifugal force which is the gravitational force. Hence,
$\Rightarrow \dfrac{{m{v^2}}}{r} = \dfrac{{GMm}}{{{r^2}}}$

Thus, the net force on the satellite is F. Hence, the correct option is Option (A).

Note:
There are three kinds of satellite orbits – Geostationary, Middle Earth Orbit, and Low Earth Orbit.
The distances of these satellite orbits from Earth are:
i) Low Earth orbit – 20,000 km
ii) Middle Earth orbit – Middle of Low Earth orbit and Geostationary orbit
iii) Geostationary orbit – 36,000 km.