Question

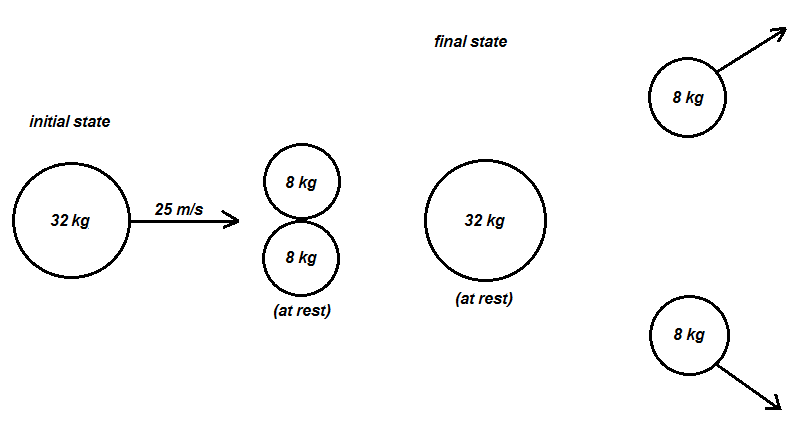
A scattering experiment is done with a \[32\,{\text{kg}}\] disc and two \[8\,{\text{kg}}\] discs on a frictionless surface. In the initial state of the experiment, the heavier disc moves in the \[x\] direction with velocity \[v = 25\,{\text{m}}{{\text{s}}^{ - 1}}\] towards the lighter discs, which are at rest. The discs collide elastically. In the final state, the heavy disc is at rest and the two smaller discs scatter outward with the same speed. What is the \[x - \] component of the velocity of each of the \[8\,{\text{kg}}\] discs in the final state?

A. \[12.5\,{\text{m}}{{\text{s}}^{ - 1}}\]
B. \[16\,{\text{m}}{{\text{s}}^{ - 1}}\]
C. \[25\,{\text{m}}{{\text{s}}^{ - 1}}\]
D. \[50\,{\text{m}}{{\text{s}}^{ - 1}}\]
E. \[100\,{\text{m}}{{\text{s}}^{ - 1}}\]

Answer 1

Hint: First of all, we will find out the momentum of the system before collision took place followed by momentum after the collision. We will equate both the momenta as momentum is conserved. We will substitute the required values and manipulate accordingly to find the result.

Complete step by step answer:In the given problem, we are supplied the following data:

The mass of the large disc is \[32\,{\text{kg}}\] .
The masses of the smaller discs are \[8\,{\text{kg}}\] each.
The plane on which the discs collide is given as frictionless i.e. there is no loss of energy.
In the first case both the smaller discs are at rest and the large disc has a velocity of \[25\,{\text{m}}{{\text{s}}^{ - 1}}\] .
However, in the second case, the large disc comes to rest after the collision and the smaller discs continue to move at certain velocity.
We are asked to find the velocity of each of the \[8\,{\text{kg}}\] discs in the final state.

To begin with, this problem is based on the conservation of linear momentum. This principle states that the momentum of the system before the collision and after the collision needs to be equal.

In the first case,
We will calculate the momentum of the system which is the sum of the momenta of the large disc and the two smaller discs.
Mathematically, we can write:
\[{p_1} = M{v_{\text{M}}} + {m_1}{v_1} + {m_2}{v_2}\] …… (1)
Where,
\[{p_1}\] indicates the momentum before collision.
\[M\] indicates the mass of the larger disc.
\[{v_{\text{M}}}\] indicates velocity of the larger disc.
\[{m_1}\] indicates the mass of one of the smaller discs.
\[{v_1}\] indicates velocity of one of the smaller discs.
\[{m_2}\] indicates mass of the second smaller disc.
\[{v_2}\] indicates the velocity of the second smaller disc.

Since, both the smaller discs are at rest initially.
Substituting the required values in equation (1) we get,
\[
  {p_1} = M{v_{\text{M}}} + {m_1}{v_1} + {m_2}{v_2} \\
  {p_1} = 32 \times 25 + 0 + 0 \\
  {p_1} = 800\,{\text{kgm}}{{\text{s}}^{ - 1}} \\
\]
For the second case, the bigger disc is at rest and the two smaller discs move at certain velocity.
Again, we calculate momentum after collision.
Let \[v\] be the common velocity of both the smaller discs.
\[
  {p_2} = M{v_{\text{M}}} + \left( {{m_1} + {m_2}} \right)v \\
  {p_2} = 32 \times 0 + \left( {8 + 8} \right)v \\
  {p_2} = 16v \\
\]
According to the principle of conservation of linear momentum, we can write:
\[
  {p_1} = {p_2} \\
  800\,{\text{kgm}}{{\text{s}}^{ - 1}} = 16v \\
  v = \dfrac{{800}}{{16}}\,{\text{kgm}}{{\text{s}}^{ - 1}} \\
  v = 50\,{\text{kgm}}{{\text{s}}^{ - 1}} \\
\]
Hence, the \[x - \] component of the velocity of each of the \[8\,{\text{kg}}\] discs in the final state is \[50\,{\text{kgm}}{{\text{s}}^{ - 1}}\] .
The correct option is D.

Note:This problem is based on the conservation of linear momentum. Momentum will always be conserved even if there are more than two discs. On colliding, the body transfers all its momentum to all the other bodies taking part. In elastic collision there is no loss of energy. In inelastic collision, the bodies stick to each other and the kinetic energy is not conserved.