Question

A school crossing sign has the dimension (in cm) as shown in the figure.

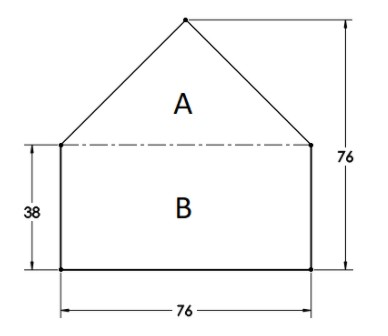
(a) What is the area of the signboard?
(b) If the $4$ such signboards are cut from the rectangular metal sheet $350cm$ long and $320cm$ wide, what will be the area of the metal left over?

Answer 1

Hint:Try to visualise the signboard as the combination of a triangle and a rectangle at the base. Now find the area of both and add them to find the area of the metal sheet required to make them.For calculating leftover from the metal sheet we should subtract the total area of four signboards from the total area of rectangular metal sheet to get the required answers.

Complete step-by-step answer:

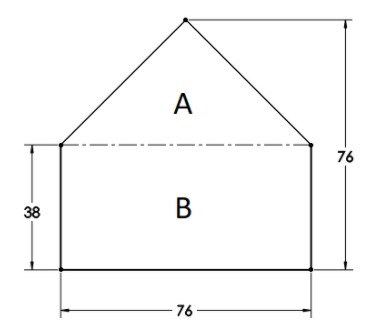
Let us draw an imaginary line which will be the base of our triangle on the upper part of the board. So, we have a triangular part (A) and a rectangular part (B)
Now it’s easier to add areas of both the areas to calculate the total area of the board
Area of signboard $ = $Area of triangle$ + $ Area of rectangle$ = $ Area of A$ + $ Area of B
Since we know the formula for the area of the triangle is half times base times altitude and area of the rectangle as length times the breadth
Therefore,
Area of signboard$ = \dfrac{1}{2} \times $ Base$ \times $ Altitude $ + $ Length$ \times $ Breadth $ = \left( {\dfrac{1}{2} \times 76 \times 38} \right) + \left( {76 \times 38} \right) = \dfrac{3}{2} \times 2888$
Area of signboard$ = 4332c{m^2}$

According to question, for calculating leftover from metal sheet we can subtract the total area of four signboards from the total area of rectangular metal sheet, i.e. :
Leftover area of metal sheet$ = $ Area of rectangular metal sheet$ - $$4 \times $ Area of signboard………..$(i)$
Given data of Metal sheet is: Length$ = 350cm$ and Breadth $ = 320cm$
After substituting all the values in the right hand side of $(i)$, we can calculate easily
Area of metal leftover$ = \left( {350 \times 320} \right) - 4 \times 4332 = 112000 - 17328 = 94672c{m^2}$

Note:Be careful with the calculation and don’t forget to use braces to avoid mistakes. An alternative approach for this problem is by drawing an imaginary perpendicular line from the top corner of the board to the middle of the baseline. This will divide the signboard into two trapeziums. And thus total area can be calculated by adding up areas of trapeziums.