Question

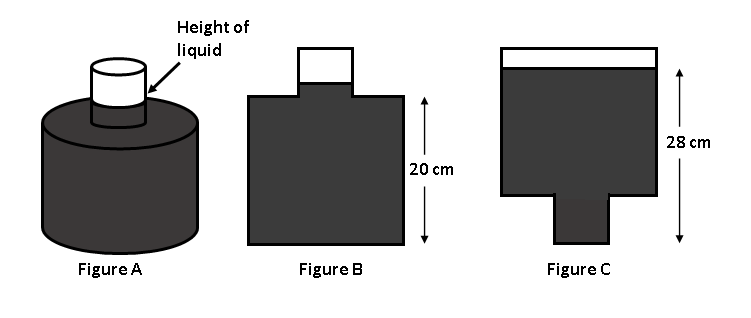
A sealed bottle, which contains water, has been constructed by attaching a cylinder of radius $1cm$ to a cylinder of radius $3cm$ , as shown in figure $A$ . When the bottle is right side up, the height of water inside is $20cm$ , as shown in the cross section of the bottle in Figure $B$ . When the bottle is upside down, the height of the liquid is $28cm$ , as shown in Figure $C$ . What is the total height, in $cm$ , of the bottle?

Answer 1

Hint: In this question, we are given a cylinder whose bottom part has radius $3cm$ and upper part has radius $1cm$ , and it is filled with some water, as shown. Now, we have to find its total height. So, let height of large cylinder be ${h_1}$ and height of small cylinder be ${h_2}$ and let total height of cylinder be $x$ , then it can be written as, $x = {h_1} + {h_2}$ . Now, we will find the volume of the unfilled part of the cylinder and equate them.
Formulae to be used:
Volume of cylinder $ = \pi {r^2}h$ .

Complete answer:
We are given a cylinder which is made by joining two cylinders, with radius of large cylinder $ = 3cm$ and volume of volume of small cylinder $ = 1cm$ .
To find the total height of the cylinder.
Let, height of large cylinder be ${h_1}$ and height of small cylinder be ${h_2}$ and let total height of cylinder be $x$ , then it can be written as, $x = {h_1} + {h_2}$ .
Now, when the container is right side up, most of it is filled with water but some part of the cylinder is unfilled, so height of unfilled part \[ = (x - 20)cm\] .
Similarly, when the container is upside down, the height of the unfilled part is given by $ = (x - 28)cm$ .
Now, we know that Volume of cylinder $ = \pi {r^2}h$ .
So, Volume of the unfilled part when it is right side up is given by $ = \pi {\left( 1 \right)^2}\left( {x - 20} \right)$ .
And Volume of the unfilled part when it is upside down is given by $ = \pi {\left( 3 \right)^2}\left( {x - 28} \right)$ .
Now clearly these two volumes will be equal so $ = \pi {\left( 1 \right)^2}\left( {x - 20} \right) = \pi {\left( 3 \right)^2}\left( {x - 28} \right)$ i.e., $x - 20 = 9\pi \left( {x - 28} \right)$ .
On solving, for $x$ , we get $x = 29cm$ .
Hence, the total height of the cylinder is $29cm$ .

Note: Since, both the cylinders are same, i.e., water filled inside it is also equal, hence, volume of unfilled part is also equal. One must know the formula of the volume of the cylinder in order to answer this question. Instead of equating volume of filled part, equating volume of unfilled part is easier to solve. Also, we have to be careful in simple calculations where we tend to make mistakes.