
A ship is travelling due east at 10km/h. A ship heading 30
Answer
515.1k+ views
Hint: A vector can be resolved into its components. This problem can be solved by resolving components of the velocities of the two ships. Equating components wherever possible may give us the required answer.
Step by step solution:
We have ship 1 travelling in the east direction with a speed of 10km/h.
The ship 2 is travelling at an angle of 30
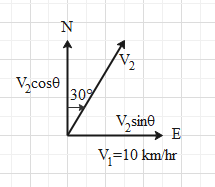
Here we have resolved the velocity
We see that component
Putting the known values, we get
This is the required value and the correct answer is option C.
Additional information:
The magnitude of a vector can be calculated from its components using the Pythagoras theorem. If a vector V has components
We can also resolve components of a vector in 3 dimensions. In case of 3-dimensional representation, the components of V would be
Note: The components of a vector are constructed using trigonometric identities which satisfy the Pythagorean Theorem for the magnitude of the vector. The components signify the directions in which a part of the main vector can be distributed and we designate those directions to be along the coordinate axes.
Step by step solution:
We have ship 1 travelling in the east direction with a speed of 10km/h.
The ship 2 is travelling at an angle of 30

Here we have resolved the velocity
We see that component
Putting the known values, we get
This is the required value and the correct answer is option C.
Additional information:
The magnitude of a vector can be calculated from its components using the Pythagoras theorem. If a vector V has components
We can also resolve components of a vector in 3 dimensions. In case of 3-dimensional representation, the components of V would be
Note: The components of a vector are constructed using trigonometric identities which satisfy the Pythagorean Theorem for the magnitude of the vector. The components signify the directions in which a part of the main vector can be distributed and we designate those directions to be along the coordinate axes.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




