
What is a simple pendulum? What type of motion does it have?
Answer
488.4k+ views
Hint: A simple pendulum is a mass (say
Complete answer:
A simple pendulum consists of a mass
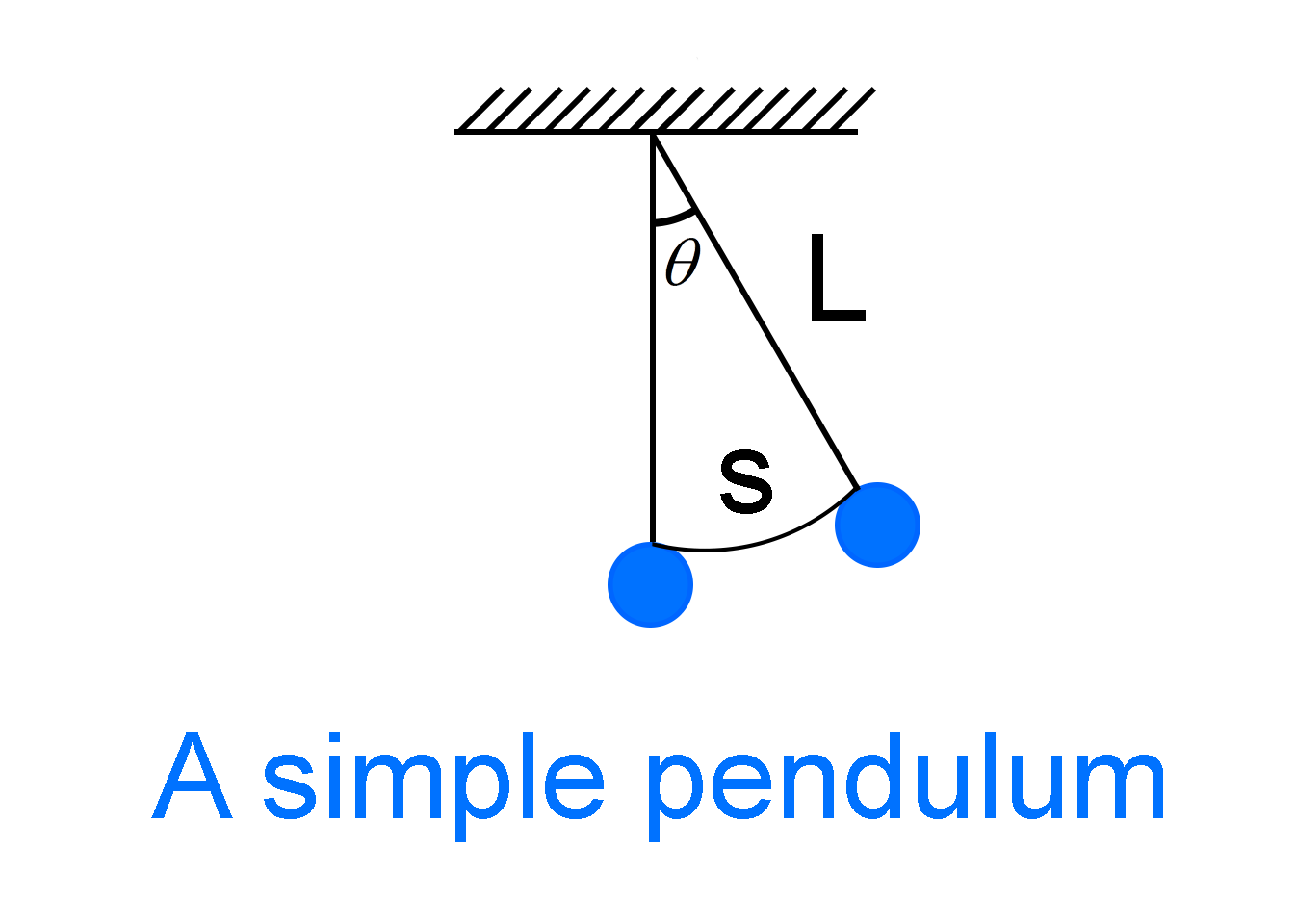
While the equation is not in the rest position a restoring force acts on the simple pendulum which tries to restore the pendulum to its rest position.
The restoring force is given by the following equation
The negative sign indicates that the force acts in a direction opposite to the movement of the pendulum.
If the displacement of the pendulum is small, then
We know that the angle that the arc makes at the pivot point is equal to
So,
We also know that the equation for restoring force for rotational motion is
Here,
Comparing equation 1 and 2, we get
We know that the equation for the time period of a pendulum is
Here,
So, for a simple pendulum, this equation becomes
The simple pendulum has a simple harmonic motion and the equation for a simple harmonic motion for a simple pendulum is
Here,
Note:
The equation for the time period that we obtained, i.e.
Complete answer:
A simple pendulum consists of a mass

While the equation is not in the rest position a restoring force acts on the simple pendulum which tries to restore the pendulum to its rest position.
The restoring force is given by the following equation
The negative sign indicates that the force acts in a direction opposite to the movement of the pendulum.
If the displacement of the pendulum is small, then
We know that the angle that the arc makes at the pivot point is equal to
So,
We also know that the equation for restoring force for rotational motion is
Here,
Comparing equation 1 and 2, we get
We know that the equation for the time period of a pendulum is
Here,
So, for a simple pendulum, this equation becomes
The simple pendulum has a simple harmonic motion and the equation for a simple harmonic motion for a simple pendulum is
Here,
Note:
The equation for the time period that we obtained, i.e.
Recently Updated Pages
Earth rotates from West to east ATrue BFalse class 6 social science CBSE

The easternmost longitude of India is A 97circ 25E class 6 social science CBSE

Write the given sentence in the passive voice Ann cant class 6 CBSE

Convert 1 foot into meters A030 meter B03048 meter-class-6-maths-CBSE

What is the LCM of 30 and 40 class 6 maths CBSE

What is history A The science that tries to understand class 6 social science CBSE

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light




