Question

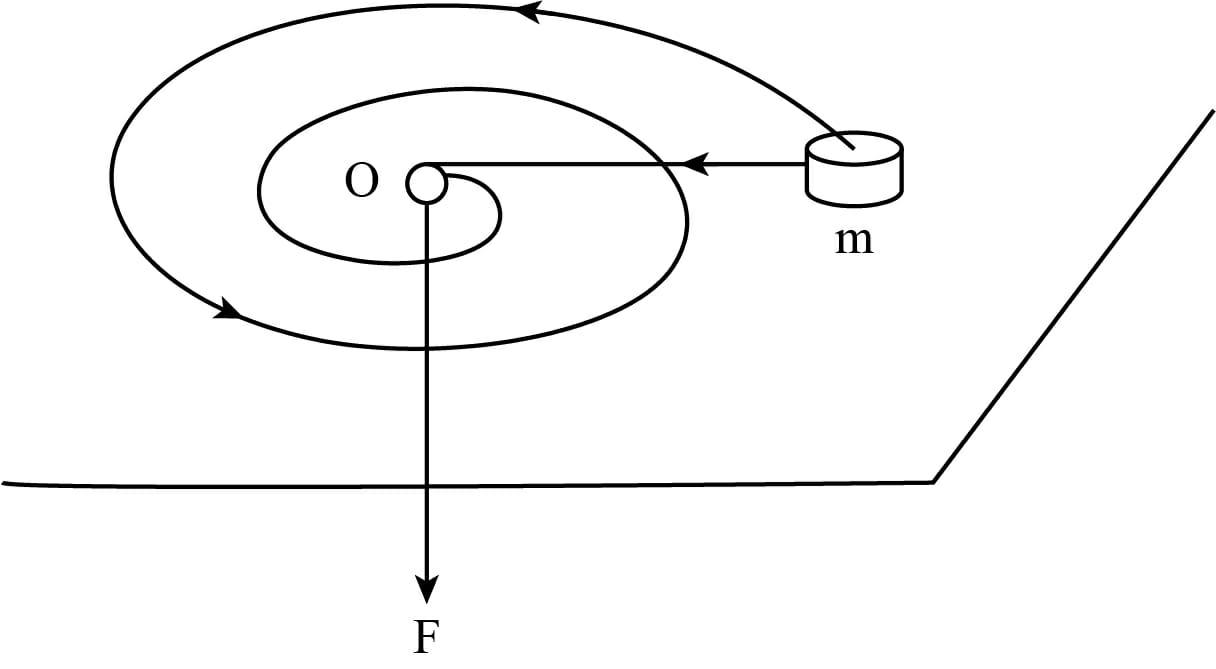
A small body of mass m tied to a non-stretchable thread moves over a smooth horizontal plane. The other end of the thread is being drawn into a hole $O$ (figure shown above) with a constant velocity. Find the thread tension as a function of the distance $r$ between the body and the hole if at $r=r_0$ the angular velocity of the thread is equal to ${\omega _o}$.

Answer 1

Hint: To solve this problem we use the concept of conservation of angular momentum since the momentum of force $T$ is also zero at the point $O$. Therefore, we can say that the angular momentum of the particle m is conserved about the centre point $O$.

Complete step by step answer:
Forces, acting on the mass m are shown in the figure. As a vector ${\text{N = mg}}$, the net torque of these two forces about any fixed point must be equal to zero. Tension T, acting on the mass m is a central force, which is always directed towards the centre O. Hence the moment of force T is also zero about the point O and therefore the angular momentum of the particle m is conserved about O.

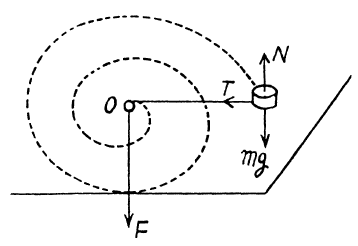
Let, the angular velocity of the particle be $\omega $, when the separation between hole and particle m is r, then from the conservation of angular momentum about the point $O$,
$\therefore {\text{m(}}{\omega _o}{{\text{r}}_o}){{\text{r}}_o} = {\text{m(}}\omega {\text{r)r}}$
Also $\omega = \dfrac{{{\omega _o}{{\text{r}}_o}^2}}{{{{\text{r}}^2}}}$
Now from the Newton’s second law of motion,
${\text{T = F = m}}{\omega ^2}{\text{r}}$
$ \Rightarrow {\text{F = }}\dfrac{{{\text{m}}{\omega _o}^2{{\text{r}}_o}^4{\text{r}}}}{{{{\text{r}}^4}}} = \dfrac{{{\text{m}}{\omega _o}^2{{\text{r}}_o}^4}}{{{{\text{r}}^3}}}$


$\therefore$ The thread tension = $\dfrac{{{\text{m}}{\omega _o}^2{{\text{r}}_o}^4}}{{{{\text{r}}^3}}}$

Note:
Law of conservation of angular momentum states that if no external torque acts on the object, then there is no angular momentum.
$\because {\text{torque (}}\tau {\text{) = }}\dfrac{{{\text{dL}}}}{{{\text{dT}}}}$
$L$ = angular momentum
Because the momentum of $\tau $ is zero.
$ \Rightarrow \tau = 0 $
$ \Rightarrow \dfrac{d\vec L}{d\vec t} = 0 $
$ \Rightarrow {\text{L = 0}}$
So, the angular momentum is conserved.
$\therefore {\text{m(}}\omega {\text{r)r = m(}}{\omega _o}{{\text{r}}_o}){{\text{r}}_o}$