
Answer
472.5k+ views
Hint: Use kinematics equation. In this question, the mostly used formula is the kinematic equation. Use time of flight formula. Also use the formula of speed. Apply the concept of perfectly elastic collision.
Step by step solution:
Diagram:
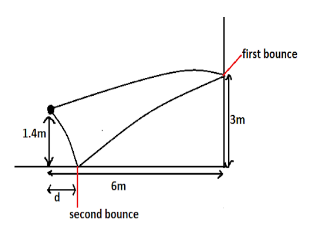
Let’s assume that boy throws the ball at a horizontal speed of u and vertical speed u.
Let the distance be h where the ball bounces off the ground.
Acceleration due to gravity is given by $g=10m/{{s}^{2}}$
We know that speed is equal to distance per unit time.
Mathematically,
$speed=\dfrac{dis\tan ce}{time}$
Now time taken by the ball to hit the wall is given by,
$t=\dfrac{6}{u}$
In this time, $\Delta y=3-1.4m$=106m
Now use kinematics equation,
$\dfrac{d}{u}$$1.6=6*\dfrac{v}{u}-5{{(\dfrac{6}{u})}^{2}}$ --------(1)
Given that collision is elastic, in this situation horizontal speed changes its speed and vertical speed remain the same.
Now time taken by the ball to reach height of 1.4m is$\dfrac{12-2d}{u}$
Use time of flight formula,
$\dfrac{v}{5}=\dfrac{12-2d}{u}$ -------(2)
Time taken to reach ground is $\dfrac{d}{u}$ and vertical speed of the ball is –v for height 1.4m
Use kinematics equation in the direction of y,
$\begin{align}
& -1.4=-v\dfrac{d}{u}-5{{(\dfrac{d}{u})}^{2}}----(3) \\
& substitute(2)in(1)and(3) \\
& we have, \\
& 1.6=\dfrac{6(60-10d)-180}{{{u}^{2}}} \\
& 1.6{{u}^{2}}=180-60d-----(4) \\
& 8.4{{u}^{2}}=(1.6{{u}^{2}}+180)d+30{{d}^{2}}----(5) \\
& substitute(4)in(5) \\
& 30{{d}^{2}}-675d+945=0 \\
& d=1.5m \\
\end{align}$
Since the value of d=21 m won’t be possible.
Note: Notice that, in the diagram there are two bounces. One on the wall and other on the ground. 6m is not a height of wall but a distance between boy and wall. You may get confused here. In this kind of question, concentration and focus are important along with a good concept. Students may get confused between kinematic equations that which kinematic equation should have to use. Do not get confused between spend and velocity as well as distance displacement.
Step by step solution:
Diagram:

Let’s assume that boy throws the ball at a horizontal speed of u and vertical speed u.
Let the distance be h where the ball bounces off the ground.
Acceleration due to gravity is given by $g=10m/{{s}^{2}}$
We know that speed is equal to distance per unit time.
Mathematically,
$speed=\dfrac{dis\tan ce}{time}$
Now time taken by the ball to hit the wall is given by,
$t=\dfrac{6}{u}$
In this time, $\Delta y=3-1.4m$=106m
Now use kinematics equation,
$\dfrac{d}{u}$$1.6=6*\dfrac{v}{u}-5{{(\dfrac{6}{u})}^{2}}$ --------(1)
Given that collision is elastic, in this situation horizontal speed changes its speed and vertical speed remain the same.
Now time taken by the ball to reach height of 1.4m is$\dfrac{12-2d}{u}$
Use time of flight formula,
$\dfrac{v}{5}=\dfrac{12-2d}{u}$ -------(2)
Time taken to reach ground is $\dfrac{d}{u}$ and vertical speed of the ball is –v for height 1.4m
Use kinematics equation in the direction of y,
$\begin{align}
& -1.4=-v\dfrac{d}{u}-5{{(\dfrac{d}{u})}^{2}}----(3) \\
& substitute(2)in(1)and(3) \\
& we have, \\
& 1.6=\dfrac{6(60-10d)-180}{{{u}^{2}}} \\
& 1.6{{u}^{2}}=180-60d-----(4) \\
& 8.4{{u}^{2}}=(1.6{{u}^{2}}+180)d+30{{d}^{2}}----(5) \\
& substitute(4)in(5) \\
& 30{{d}^{2}}-675d+945=0 \\
& d=1.5m \\
\end{align}$
Since the value of d=21 m won’t be possible.
Note: Notice that, in the diagram there are two bounces. One on the wall and other on the ground. 6m is not a height of wall but a distance between boy and wall. You may get confused here. In this kind of question, concentration and focus are important along with a good concept. Students may get confused between kinematic equations that which kinematic equation should have to use. Do not get confused between spend and velocity as well as distance displacement.
Recently Updated Pages
Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which are the Top 10 Largest Countries of the World?

How do you graph the function fx 4x class 9 maths CBSE

Who was the leader of the Bolshevik Party A Leon Trotsky class 9 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Which is the largest saltwater lake in India A Chilika class 8 social science CBSE

Ghatikas during the period of Satavahanas were aHospitals class 6 social science CBSE




