Question

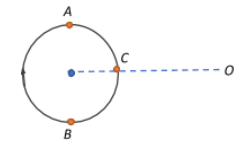
A small source of sound moves on a circle as shown in the figure, and an observer is sitting at 0. Let $\nu_1, \nu_2, \nu_3$ be the frequencies heard when the source is at A, B and C respectively. Then,

A. $\nu_1> \nu_2> \nu_3$
B. $\nu_1 =\nu_2 >\nu_3$
C. $\nu_2> \nu_3> \nu_1$
D. $\nu_1 >\nu_3> \nu_2$

Answer 1

Hint: Try and recall the trend of frequency change with respect to a relative motion between the source and the observer. In other words, we can use the principle of Doppler effect, which states that if a sound wave source is moving towards or away from an observer its frequency as heard by the observer will be greater than or less than the original frequency respectively. Use this to determine the frequency of the sound wave at different points in the source path by deducing the direction of motion of the sound wave at those points, relative to the observer.

Complete answer:
We can easily deduce the relation between the change in the frequency of the sound heard by the observer with the motion of the sound source by understanding the Doppler Effect.
Doppler effect describes the change in the pitch (frequency) of sound waves whenever the source of sound and the observer are in relative motion. It suggests that whenever the source approaches a stationary observer, the apparent frequency (as heard by the observer) will be more than the actual frequency, and whenever the source is receding from a stationary observer, the apparent frequency will be less than the actual frequency.
In this context let us look at the question. The frequency of sound as heard by the observer when the source is at C is $\nu_3$.

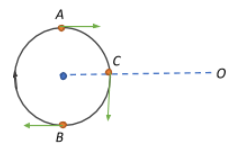
When the source is at C, the sound wave moves perpendicular to the line joining the source and the observer, so there is no relative motion between the sound wave and the observer . This means that the frequency of sound heard by the observer when the source is at C will be the same as the original frequency $\nu_0 = \nu_3$.
Now, assume that that source is moving through B. This means that the source is moving away from the observer. Thus, the frequency of sound as heard by the observer when the source is at B will be less than what they heard when the source was at C, i.e., $\nu_2<\nu_3$.
This also means that $\nu_2<\nu_1$ since at point A we see that the source is not receding from the observer.
Now, as the source moves from B to A its motion is directed towards the source. This means that the frequency of sound heard by the observer when source is at A will be $\nu_1>\nu_2$, and since the sound speed is directed towards the observer, it will have a greater frequency than the original frequency, i.e., $\nu_1>\nu_0 \Rightarrow \nu_1 >\nu_3$
Thus, we have $\nu_2<\nu_3$ and $\nu_1>\nu_3$ which means that
$\nu_1>\nu_3>\nu_2$.

Thus, the correct choice would be D. $\nu_1>\nu_3>\nu_2$.

Note:
Remember that this deduction of the change in frequency with a relative motion between the source and the observer is applicable as long as the wave speed of the source is less than the speed of sound in the given medium. When the source travels with a wave speed greater than speed of sound (i.e., at supersonic speed) the waves pile up and produce a shock wave or a Mach wave, which produces a loud and violent sound called the sonic boom (that we hear when a supersonic plane passes by).
Also, do not forget that there is no change in the frequency if the source and the observer move in the same direction with the same speed, or when either the source or the observer is at the centre of a circle and the other moves around it, or if both the source and observer are at rest and only the medium between them is in motion.