Question

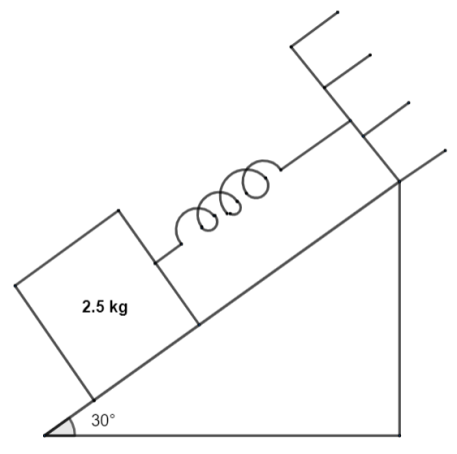
A smooth inclined plane having angle of inclination ${{30}^{\text{o}}}$ with horizontal has a mass 2.5 kg is held by a spring which is fixed at the upper end as shown in figure. If the mass is taken 2.5 cm up along the surface of the inclined plane, the tension in the spring reduces to zero, if the mass is then released, the angular frequency of oscillation I radian per second is

$\left( a \right)0.707$
$\left( b \right)7.07$
$\left( c \right)1.414$
$\left( d \right)14.14$

Answer 1

Hint: We will use the formula of angular velocity as the surface is of the inclined plane. It is clear from the question that there is no tension on the spring so, by the use of the direct formula of induced force equal to force of inclination will be useful for angular frequency.

Formula used:
$\omega =\sqrt{\dfrac{K}{m}},F=mg\sin \left( \theta \right),K\times x=mg\sin \left( \theta \right)$ where m is the mass of the object, K is spring constant; g is gravitational force, $\theta $ is the angle inclined and $\omega $ is angular velocity.

Complete answer:
Angular frequency: By the term angular frequency we mean the number of events that are occurring per unit time.

As the weight attached to the spring with a mass of 2.5 kg does create tension in the spring. But in the question it is given that the tension is reduced to zero. This results in the fact that the string is not at all stretched. As the force created is with an angle ${{30}^{\text{o}}}$ so, the acceleration of the spring is going to be equal to $g\sin \left( {{30}^{\text{o}}} \right)$. This gives the force to be equal to

$\begin{align}
  & F=ma \\
 & \Rightarrow F=mg\sin \left( {{30}^{\text{o}}} \right) \\
\end{align}$

This force will be further equal to the spring constant, the product of the spring constant and the extension of the spring. Therefore, $K\times x=mg\sin \left( {{30}^{\text{o}}} \right)$ .
Since, the mass of the object is 2.5 cm or 0.025 m upwards but along the surface of the inclined plane, so the extension of spring due to the mass x = 0.025 m.
As, $\sin \left( {{30}^{\text{o}}} \right)=\dfrac{1}{2}$
Thus,
\[\begin{align}
  & K\times x=mg\sin \left( {{30}^{\text{o}}} \right) \\
 & \Rightarrow K\times 0.025=2.5\left( 10 \right)\left( \dfrac{1}{2} \right) \\
 & \Rightarrow K=\dfrac{2.5\left( 5 \right)}{0.025} \\
 & \Rightarrow K=500 \\
\end{align}\]

Since, the force is at some angle so, there will be an angular velocity

$\begin{align}
  & \omega =\sqrt{\dfrac{K}{m}} \\
 & \Rightarrow \omega =\sqrt{\dfrac{500}{2.5}} \\
 & \Rightarrow \omega =\sqrt{200} \\
 & \Rightarrow \omega =14.14 \\
\end{align}$

By the SI unit of angular velocity to be $rad\,{{s}^{-1}}$ we get $\omega =14.14\,rad\,{{s}^{-1}}$.
Hence, the correct option is $14.14$.

So, the correct answer is “Option D”.

Note:
To solve such type of questions one should remember the following points:
(1) There can be confusion between the values of the spring constant K and its extension by the mass so, for this we will check the units here. Since, the unit of mass is used as kg and extension has used cm as a unit so, the confusion will get resolved.
(2) The concept of angular frequency must be on fingertips.
(3) Always remember the SI unit of angular velocity as $rad\,{{s}^{-1}}$.