Question

A soap (\[C_{17}H_{35}COONa\]) solution becomes a colloidal sol at a concentration of \[1.2 \times {10^3}M\].On the average,\[2.4 \times {10^{13}}\] colloidal particles are present in \[1m{m^3}\]. What is the average number of stearate ions ( in multiples of ${10^6}$) in one colloidal particle ( micelle)?
A. \[30\]
B. \[40\]
C. \[50\]
D. \[60\]

Answer 1

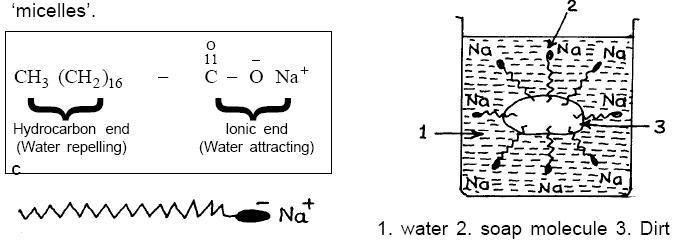
Hint: To solve this question, we first need to understand the mentioned terms like colloidal particles and also the concept of micelle. Oke, let me explain. Substances act as normal electrolyte at lower concentration but association of particles takes place at higher concentration and thus forming colloids also known as associate colloids or micelles. The cleansing act of soaps is due to the formation of micelles . Let’s understand how? When the concentration of soap in water is low, the soap particles act as electrolytes. The moment the concentration of soap particles is increased , the soap molecules arrange themselves into tiny clusters ( called micelles). The hydrophilic( water loving) part of soap molecules points outwards towards water forming the outer surface of micelle. Whereas the hydrophobic ( water hating) part of the soap molecule gets attached to oil and dirt of our body. Thus washing the soap from our body makes us clean. Let’s understand from the diagram below.

Complete step by step answer:
Given concentration or molarity(\[M\]) of the colloidal sol \[ = 1.2 \times {10^3}M\]
Given , volume(\[V\]) \[ = 1m{m^3}\]\[ = {10^{ - 6}}L\]
Therefore, number of moles(\[n\]) =\[M \times V\]
\[ = \] \[1.2 \times {10^3} \times {10^{ - 6}} = 1.2 \times {10^{ - 3}}\]
We know that \[1\] mole of soap = \[6.023 \times {10^{23}}\] molecules
Now, number of stearate ions = \[1.2 \times {10^{ - 3}} \times 6.023 \times {10^{23}} = 7.227 \times {10^{20}}\]
Therefore , average number of stearate ions in one colloidal particle( micelle)
=\[\dfrac{{7.227 \times {{10}^{20}}}}{{2.4 \times {{10}^{13}}}}\]=\[3 \times {10^7}\](approximately)
Here, \[2.4 \times {10^{13}}\] is the average number of colloidal particles present in the given volume.
But, we have to find the answer in multiples of ${10^6}$, so the desired answer should be
\[\dfrac{{3 \times {{10}^7}}}{{{{10}^6}}} = 30\]
So, the answer is Option (A) \[30\].

Note:
The CMC( critical micelle concentration) is the minimum concentration of surfactant in a bulk phase above which micelles start to form. Another important term you should know about is Kraft temperature . This is the temperature at which the solubility of a surfactant is equal to surfactant’s critical micelle concentration at the same temperature.