Question

A solid cylinder is rolling without slipping on a plane having an inclination $ \theta $ and the coefficient of static friction $ {\mu _s} $ . The relation between $ \theta $ and $ {\mu _s} $ is
(A) $ \tan \theta > 3{\mu _s} $
(B) $ \tan \theta < 3{\mu _s} $
(C) $ \tan \theta < 3{\mu _s}^2 $
(D) None of these

Answer 1

Hint: to solve this question, draw the figure of a cylinder rolling on an inclined plane and break the forces acting on the cylinder into different components. Then use the concepts of center of mass, the moment of inertia, and torque acting on a rolling body to arrive at the equation of force. Use this equation to get the answer.

Complete step by step answer:
Let the radius of the cylinder be $ R $ and the mass be $ M $ .
Let us consider a figure of an inclined plane with $ \theta $ angle at the horizontal, with a cylinder rolling on it.
We will break the forces acting on the cylinder into components of weight due to gravity as $ mg\sin \theta $ and $ mg\cos \theta $ , normal reaction force $ N $ , and resistive frictional force $ f $ as shown in the figure.

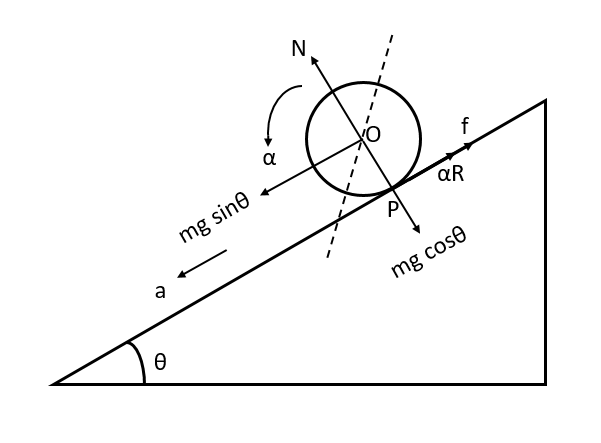
Since this is a case of pure rolling, there is a presence of angular acceleration $ \alpha $ for the rotational motion, and a linear acceleration $ a $ for the translational motion of the cylinder.
At the point of contact $ P $ from where the rolling starts, we can say that the velocity is zero.
Hence acceleration $ a $ along the surface at $ P $ is also zero.
 $ \therefore {\vec a_P} = 0 $ ………….. $ (1) $
Also, we can say that acceleration at $ P $ ,
 $ {\vec a_P} = {\vec a_{P|COM}} + {\vec \alpha _{COM}} $ ………….. $ (2) $
where, $ {\vec a_{P|COM}} = $ acceleration of $ P $ with respect to center of mass,
 $ {\vec \alpha _{COM}} = $ acceleration of center of mass with respect to the ground.
About the center of mass every point on the cylinder undergoes a circular motion with an angular acceleration $ \alpha $ towards the tangential direction. Hence,
 $ {\vec a_{P|COM}} = \vec \alpha R( \to ) $
Acceleration of center of mass with respect to the ground is $ \vec a $ towards the opposite direction. Hence,
 $ {\vec \alpha _{COM}} = \vec a( \leftarrow ) $
Therefore, from equation $ (1) $ and $ (2) $ we get,
 $ \vec \alpha R( \to ) + \vec a( \leftarrow ) = 0 $
Since both the quantities are in the opposite direction,
 $ \vec a = \vec \alpha R $ ………….. $ (3) $
Now let us write the equation of force along the inclined plane,
 $ mg\sin \theta - f = ma $ ………….. $ (4) $
Due to the presence of friction, there will be a torque acting about the point $ O $ .
We know that, torque $ \vec \tau = \vec r \times \vec F $ ,
where $ \vec r $ is the position vector.
Therefore, the torque about $ mg\sin \theta $ , $ mg\cos \theta $ and $ N $ will be $ 0 $ .
While the torque for friction is given as, $ \tau = fR $ , since the line of friction and radius from the center is perpendicular.
Considering the moment of inertia, $ I $ about the axis of the torque taken we get,
 $ fR = I\alpha $
We know that moment of inertia for a cylinder, $ I = \dfrac{{m{R^2}}}{2} $ .
 $ \therefore fR = \dfrac{{m{R^2}}}{2}\alpha $
Cancelling $ R $ from both sides we get,
 $ f = \dfrac{{mR\alpha }}{2} $
From equation $ (3) $ we get,
 $ f = \dfrac{{ma}}{2} $ ………….. $ (5) $
Putting this value in equation $ (4) $ we get,
 $ mg\sin \theta - \dfrac{{ma}}{2} = ma $
 $ \Rightarrow mg\sin \theta = \dfrac{{ma}}{2} + ma $
Upon further solving we get,
 $ mg\sin \theta = \dfrac{3}{2}ma $
Cancelling $ m $ from both sides we get,
 $ g\sin \theta = \dfrac{3}{2}a $
 $ \Rightarrow a = \dfrac{2}{3}g\sin \theta $
Putting this value of $ a $ in equation $ (5) $ we get,
 $ f = \dfrac{m}{2} \times \dfrac{2}{3}g\sin \theta $
 $ \Rightarrow f = \dfrac{{mg\sin \theta }}{3} $ ………….. $ (6) $
Therefore, this must be the value of friction for pure rolling.
Therefore, $ {f_{\max }} = {\mu _s}N $
When $ \theta $ is maximum from the figure we get, $ N = mg\cos \theta $
Hence $ {f_{\max }} = {\mu _s}mg\cos \theta $ ………….. $ (7) $
Upon equating equation $ (6) $ and $ (7) $ we get,
 $ {\mu _s}mg\cos \theta = \dfrac{{mg\sin \theta }}{3} $
Cancelling out $ mg $ from both sides we get,
 $ {\mu _s}\cos \theta = \dfrac{{\sin \theta }}{3} $
 $ \Rightarrow \tan \theta = 3{\mu _s} $
This is the condition for maximum friction for pure rolling.
Hence option (2) is the correct answer.

Note:
Be careful of the direction or the lines of forces acting on the cylinder. Proper identification of the directions can help us solve the question easily up to a great deal. Mistakes regarding direction can be reduced by drawing a figure of the setup.