Question

A solid cylinder of height H and density \[\rho \] is floating in a non-viscous liquid of density \[{{\rho }_{0}}\] as shown in the figure. IN equilibrium condition a length h of the cylinder is inside the liquid. If it is displaced slightly from that position then the time period of the oscillating cylinder is –

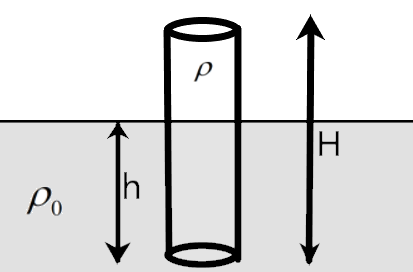
\[\begin{align}
  & \text{A) 2}\pi \sqrt{\dfrac{H}{g}} \\
 & \text{B) 2}\pi \sqrt{\dfrac{h}{g}} \\
 & \text{C) 2}\pi \sqrt{\dfrac{\rho h}{{{\rho }_{0}}g}} \\
 & \text{D) 2}\pi \sqrt{\dfrac{{{\rho }_{0}}H}{\rho g}} \\
\end{align}\]

Answer 1

Hint: We need to understand the relation between the force acting on the cylinder and the force due to the mass of the cylinder which cancels off at the equilibrium condition. A displacement will result in the oscillation of the system in the liquid.

Complete step-by-step solution
 We know that for an object to be partially immersed in a fluid as per the given situation, the weight due to the mass of the cylinder is balanced by the buoyancy applied by the liquid on the cylinder.

We can give this relation mathematically as –
\[{{F}_{eqm}}=W-B=0\]
Now, when the cylinder is provided with a small displacement of ‘x’, the buoyancy acting will increase with the mass immersed in the liquid during the oscillation. The buoyant force will be proportional to the volume occupied by the cylinder and the density of the liquid. This can be given as –
\[{{B}_{new}}=V.{{\rho }_{0}}.g\]
Where V is the extra volume immersed in the liquid.
Now, the net force acting on the cylinder will be excess due to the buoyancy, which is given as –
\[\begin{align}
  & {{F}_{net}}=-{{B}_{new}} \\
 & \Rightarrow {{F}_{net}}=-V{{\rho }_{0}}g \\
\end{align}\]
Now, we can substitute the volume in terms of area A and x as the displacement of the cylinder during its oscillation. We can write this as –
\[\begin{align}
  & {{F}_{net}}=-V{{\rho }_{0}}g \\
 & \Rightarrow {{F}_{net}}=-Ax{{\rho }_{0}}g \\
\end{align}\]
We know that this force causes an acceleration due to oscillation in the cylinder which can be substituted for the net force as –
\[\begin{align}
  & {{F}_{net}}=ma \\
 & \text{but,} \\
 & \text{Density}=\dfrac{\text{Mass}}{\text{Volume of the cylinder in equilibrium}} \\
 & \Rightarrow m=\rho Ah \\
 & \text{Now,} \\
 & \Rightarrow {{F}_{net}}=(\rho Ah)a \\
\end{align}\]
We can equate the net forces to get the acceleration of the cylinder with the displacement ‘x’ about its mean position as –
\[\begin{align}
  & ma=-Ax{{\rho }_{0}}g \\
 & \Rightarrow (\rho Ah)a=-Ax{{\rho }_{0}}g \\
 & \Rightarrow a=\dfrac{-x{{\rho }_{0}}g}{\rho h}\text{ --(1)} \\
\end{align}\]
Now, we know that the linear acceleration ‘a’ in a SHM is related to the angular frequency, which in turn is related to the time period T as –
\[\begin{align}
  & a=-{{\omega }^{2}}x\text{ --(2)} \\
 & \text{but,} \\
 & \omega =\dfrac{2\pi }{T} \\
 & \Rightarrow T=\dfrac{2\pi }{\omega } \\
 & \text{From (2),} \\
 & a=-{{\omega }^{2}}x \\
 & \Rightarrow a=-{{(\dfrac{2\pi }{T})}^{2}}x \\
 & \Rightarrow {{T}^{2}}=-\dfrac{4{{\pi }^{2}}x}{a} \\
 & \text{substituting from (1) gives,} \\
 & {{T}^{2}}=-\dfrac{4{{\pi }^{2}}x}{(-x\dfrac{{{\rho }_{0}}g}{\rho h})} \\
 & \Rightarrow {{T}^{2}}=\dfrac{4{{\pi }^{2}}}{(\dfrac{{{\rho }_{0}}g}{\rho h})} \\
 & \therefore T=2\pi \sqrt{\dfrac{\rho h}{{{\rho }_{0}}g}} \\
\end{align}\]
From this, we get the time period of oscillation of the cylinder in the liquid.
The correct answer is option C.

Note: The buoyant force acting on a body in a fluid is the upward force experienced by the body in the fluid due to the pressure exerted by the molecules in it. The buoyancy is related to the density of the fluid medium and the density of the object immersed.